Como usar esta calculadora de teste t para uma amostra

Mais sobre a Teste t para uma média para que você possa interpretar melhor os resultados obtidos por este solucionador: Um teste t para uma média é um teste de hipótese que tenta fazer uma afirmação sobre a média da população ($\sigma$). Este teste t, ao contrário do teste z, não precisa saber o desvio padrão da população $\sigma$.

Como conduzir um teste t para a média de uma população?

O teste possui duas hipóteses complementares, a nula e a alternativa. A hipótese nula é uma afirmação sobre a média da população, sob a hipótese de nenhum efeito, e a hipótese alternativa é a hipótese complementar à hipótese nula. As principais propriedades de um teste t de uma amostra para uma média populacional são:

• Para um teste t para uma média, a distribuição de amostragem usada para a estatística do teste t (que é a distribuição da estatística do teste sob a suposição de que a hipótese nula é verdadeira) corresponde à distribuição t, com n-1 graus de liberdade (em vez de ser a distribuição normal padrão, como no caso de um teste z para uma média)


• Dependendo do nosso conhecimento sobre a situação "sem efeito", o teste t pode ser bicaudal, esquerdo ou direito


• O principal princípio do teste de hipótese é que a hipótese nula é rejeitada se a estatística de teste obtida for suficientemente improvável sob a suposição de que a hipótese nula é verdadeira


• O valor p é a probabilidade de obter resultados amostrais tão extremos ou mais extremos do que os resultados amostrais obtidos, assumindo que a hipótese nula é verdadeira


• Em um teste de hipóteses, existem dois tipos de erros. O erro tipo I ocorre quando rejeitamos uma hipótese nula verdadeira, e o erro tipo II ocorre quando deixamos de rejeitar uma hipótese nula falsa

Como calcular a estatística t para uma amostra?

Então, qual é a fórmula do teste t de uma amostra? Neste caso, para esta fórmula de teste t para a estatística t é

$$t = \frac{\bar X - \mu_0}{s/\sqrt{n}}$$

A hipótese nula é rejeitada quando a estatística t está na região de rejeição, que é determinada pelo nível de significância ($\alpha$), o tipo de cauda (bicaudal, caudal esquerdo ou caudal direito) e o número de graus de liberdade $df = n - 1$>

O que acontece com o teste t quando tenho 2 amostras

Observe que esta é uma calculadora de teste t de uma amostra. Se, em vez disso, você precisar comparar duas médias, deverá usar um teste t para amostras independentes , em vez de.

De maneira semelhante, você pode ter duas amostras, mas elas são emparelhadas, combinadas ou repetidas; nesse caso, a ferramenta apropriada a ser usada é esta calculadora de teste t pareado , quando for o caso.

Decisão para um teste t de uma amostra

Como você toma uma decisão sobre um teste t de uma amostra? Primeiro, você precisa conhecer a estatística t, que chamamos de $t_{obs}$, e os graus de liberdade df, para poder calcular o valor p.

O processo de cálculo do p-value dependerá do tipo de caudas definido. Para um teste bicaudal, o valor-p é calculado como $p = \Pr(|t_{df}| > |t_{obs}|)$. Então, para um teste de cauda esquerda, o valor-p é calculado como $p = \Pr(t_{df} < t_{obs})$, e para um teste de cauda direita, o valor-p é calculado como $p = \Pr(t_{df} > t_{obs})$.

Um exemplo de teste t de amostra

Uma vendedora tem registros que mostram que o cliente médio gasta em média US$ 80 em sua loja, mas recentemente ela sente que esse valor aumentou. Ela coleta uma amostra aleatória de n = 30 clientes e descobre que o valor médio gasto na loja foi de $ 85,4, com um desvio padrão amostral de $ 12,4. Ela tem evidências suficientes para afirmar que a média gasta em sua loja aumentou significativamente, no nível de significância de 0,05?

Solução:

Foram fornecidas as seguintes informações:

Hypothesized Population Mean $(\mu)$ =	$80$
Sample Standard Deviation $(s)$ =	$12.4$
Sample Size $(n)$ =	$30$
Sample Mean $(\bar X)$ =	$85.4$
Significance Level $(\alpha)$ =	$0.05$

(1) Hipóteses Nula e Alternativa

As seguintes hipóteses nula e alternativa precisam ser testadas:

$$\begin{array}{ccl} H_0: \mu & = & 80 \\\\ \\\\ H_a: \mu & > & 80 \end{array}$$

Isso corresponde a um teste de cauda direita, para o qual será utilizado um teste t para uma média, com desvio padrão populacional desconhecido, usando o desvio padrão amostral.

(2) Região De Rejeição

Com base nas informações fornecidas, o nível de significância é $\alpha = 0.05$ e o valor crítico para um teste à direita é $t_c = 1.699$.

A região de rejeição para este teste de cauda direita é $R = \{t: t > 1.699\}$

(3) Estatísticas De Teste

A estatística t é calculada da seguinte forma:

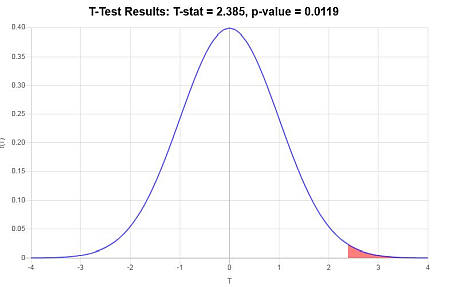
$$\begin{array}{ccl} t & = & \displaystyle \frac{\bar X - \mu_0}{s/\sqrt{n}} \\\\ \\\\ & = & \displaystyle \frac{ 85.4 - 80}{ 12.4/\sqrt{ 30}} \\\\ \\\\ & = & 2.385 \end{array}$$

(4) Decisão sobre a hipótese nula

Visto que se observa que $t = 2.385 > t_c = 1.699$, conclui-se então que a hipótese nula é rejeitada.

Usando a abordagem do valor-P: O valor-p é $p = 0.0119$, e desde $p = 0.0119 < 0.05$, conclui-se que a hipótese nula é rejeitada.

(5) Conclusão

Conclui-se que a hipótese nula Ho é rejeitado. Portanto, não há evidências suficientes para afirmar que a média populacional $\mu$ é maior que 80, no nível de significância $\alpha = 0.05$.

Intervalo De Confiança

O intervalo de confiança de 95% é $80.77 < \mu < 90.03$.

Graficamente