Regras dos Expoentes
As operações com expoentes estão entre as operações mais comuns que você realizará no Math, e é fundamental que você tenha uma base adequada sobre elas.
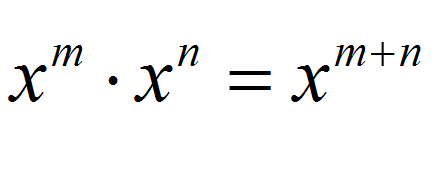
Sem mais delongas, vamos listar as propriedades básicas do expoente. Usar essas propriedades com proficiência é de extrema importância. As regras são:
Regra 1: \(\large \displaystyle x^0 = 1\), para \(x = \not 0\)
Regra 2: \(\large\displaystyle x^1 = x\)
Regra 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Regra 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Regra 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Regra 6: \(\large\displaystyle (x \cdot y)^m = x^m \cdot y^m\)
Vamos explicar um pouco essas regras em palavras .
Regra 1
está dizendo que qualquer coisa elevada à potência de zero é igual a 1. Bem, exceto 0, porque por convenção (e há uma boa razão para isso) \(0^0 = 0\).
Agora,
Regra 2
está dizendo que pegar qualquer número e elevá-lo à potência de 1 resulta no mesmo número original. Em outras palavras, elevar um número à potência de 1 não afeta o número.
Regra 3
está dizendo que quando eu multiplico potências com a mesma base, o resultado é uma potência que tem a mesma base, elevada a uma potência que corresponde à soma dos expoentes das potências que estou multiplicando.
Regra 4
está dizendo que tomar o poder de uma potência é o mesmo que tomar uma potência com os expoentes multiplicados como o expoente.
Regra 5
está dizendo que quando divido potências com a mesma base, o resultado é uma potência que tem a mesma base, elevada a uma potência que corresponde à subtração dos expoentes das potências que estou multiplicando.
Regra 6
está dizendo que quando eu tenho um poder afetando uma multiplicação, então é o mesmo que multiplicar cada um dos termos elevados a esse poder.
EXEMPLO 1
Simplifique a seguinte expressão
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2}\]RESPONDA:
Usando a Regra 5 para a divisão de poderes com a mesma base:
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2} = \frac{x^{3}y^{3}}{x^{1/2} y^2} \] \[\large \displaystyle = \frac{x^3}{x^{1/2}} \cdot \frac{y^3}{y^2} = \displaystyle x^{3-1/2} \cdot y^{3-2}\] \[\large \displaystyle = \displaystyle x^{5/2} \cdot y^{1} = x^{5/2} y\]Devo me preocupar com os expoentes negativos?
Na verdade não. Em primeiro lugar, as 5 regras para expoentes declaradas acima não fazem qualquer declaração específica sobre que os expoentes precisam ser não negativos. Na verdade, as regras funcionam da mesma forma, os expoentes são negativos.
Na verdade, para expoentes negativos , haverá duas regras que permitirão que você os transforme em expoentes positivos:
\[\large\displaystyle \frac{1}{x^n} = x^{-n}\]
A expressão acima está nos mostrando que podemos converter uma potência com um expoente negativo que está no numerador em uma potência no denominador com o expoente positivo correspondente.
Esta expressão acima está nos mostrando que podemos converter uma potência com um expoente negativo que está no denominador em uma potência no numerador com o expoente positivo correspondente.
EXEMPLO 2
Simplifique a seguinte expressão, sem deixar expoentes negativos:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}}\]RESPONDA:
Transformar os expoentes negativos em expoentes positivos e aplicar as 5 regras de expoentes:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}} = \frac{x^{4} x^{1/2} y^{-2}}{x^{-3/2} y^{1/2}} \] \[\large \displaystyle = \frac{x^{4} x^{1/2} x^{3/2}}{y^{1/2} y^{2}} = \frac{x^{4+1/2+3/2}}{y^{2+1/2}} \] \[\large \displaystyle = \frac{x^{6}}{y^{5/2}} \]que conclui a simplificação.
Essas regras de expoentes estão de alguma forma relacionadas às regras de logaritmos?
Absolutamente! Confira a regras logarítmicas e você descobrirá que eles são estruturalmente muito semelhantes, e isso porque os logaritmos e as potências são operações inversas entre si.
Apenas como uma pequena amostra, vamos fazer uma prova rápida. Suponha que \(a = x^m\) e \(b = x^n\). Então, por definição, \(m = \log_x a\) e \(n = \log_x b\). Então, pelas regras do expoente, \(a\cdot b = x^m \cdot x^n = x^{m+n}\). Portanto, por definição, \(m + n = \log_x (a \cdot b)\). Mas \(m = \log_x a\) e \(n = \log_x b\), então \(\log_x a + \log_x b = \log_x (a \cdot b)\).
Mais sobre a regra dos expoentes
Uma coisa em que precisamos enfatizar é o fato de que as regras para expoentes não exigem que os expoentes sejam positivos. Os expoentes não precisam ser inteiros. As regras valem para expoentes reais.
• Não se esqueça que se você estiver lidando com um expoente negativo no numerador, você pode transformá-lo passando para o denominador com expoente positivo.
• Além disso, se estiver lidando com um expoente negativo no denominador, você pode transformá-lo passando-o para o numerador com expoente positivo.
As regras de expoentes têm tantas aplicações, incluindo o fornecimento de uma base para a obtenção do regras para simplificar radicais , que vêm como um corolário das raízes dos expoentes.
Em termos gráficos, você pode explorar esta regra por representar graficamente diferentes funções exponenciais e ver as propriedades específicas que eles possuem.