Regras de registro
A função logarítmica é uma das funções mais importantes do Math, e as regras de log são simples e convenientes, tornando muito fácil trabalhar com logaritmos.
Vamos primeiro lembrar qual é o significado de \(\log_b a\). Neste contexto, o valor \(b\) é o base do logaritmo, e \(a\) é o argumento .
Dizemos que \(\log_b a = y\) quando \(b^y = a\). Isso significa que \(\log_b a\) é o número ao qual \(b\) (a base) precisa ser elevado para obter \(a\) (o argumento).
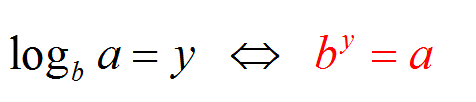
Por exemplo, \(\log_{10} 25\) corresponde ao número para o qual preciso aumentar 10, a fim de obter 25. portanto, o logaritmo que estou procurando é o número \(y\) que tem uma propriedade \(10^y = 25\)
Agora a questão é: como calculamos esse número \(y\) que tem a propriedade \(10^y = 25\)? Bem, esse número está bem definido e uma função logarítmica \(f(x) = \log_{10} x\) cuida disso. Esta função não é uma função elementar, e uma série de Taylor (série infinita) é necessária para representá-la.
Ou você pode usar uma (calculadora que provavelmente é mais fácil, certo?).
As regras do log: propriedades dos logaritmos
Estas são as principais regras de registro:
Regra 1 : \(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
Regra # 2 : \(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
Regra # 3 : \(\large \log_a (b^c) = c \cdot \log_a (b) \)
Regra # 4 : \(\large \log_a (a) = 1 \)
Regra # 5 : \(\large \log_a (1) = 0 \)
EXEMPLO 1
Simplifique \(\log_2 8 + \log_2 4\) usando regras de registro:
RESPONDA:
Usando a regra nº 1, descobrimos que:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]Portanto, a primeira etapa é uma aplicação simples da Regra nº 1, mas como obtemos \(\log_2 32 = 5\)? É porque \(2^5 = 32\), então, neste caso, encontramos diretamente qual é o número que você precisa aumentar \(2\) para obter \(32\).
Na maioria dos logaritmos, você precisa de uma calculadora para computá-los. É apenas alguns selecionados que você pode calcular diretamente. Coisas como \(\log_{10} 100 = 2\), porque você sabe facilmente que \(10^2 = 100\).
Mas, você pode calcular \(\log_{10} 102\) diretamente? Na verdade não, você precisa de uma calculadora para isso.
EXEMPLO 2
Expresse a soma e subtração dos logaritmos: \( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \).
RESPONDA:
Em primeiro lugar, precisamos lembrar que obter uma raiz cúbica é como elevar à potência \(1/3\). Em outras palavras, \(\sqrt[3]{x}\) é o mesmo que \(x^{1/3}\).
Então, primeiro associado a Regra nº 3 para colocar o poder na frente do logaritmo e, em seguida, conhecido como Regras nº 1 e 2. Nós temos:
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]que é o que era necessário: soma e subtrações de logaritmos simples.
A Mudança da Fórmula Base para Logaritmos
Uma das fórmulas mais úteis relacionadas aos logaritmos é a mudança da fórmula de base. Esta fórmula é assim:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]Esta fórmula está apenas dizendo que se você quiser mudar a base de \(b\) para \(c\), os resultados são essencialmente os mesmos, mas você precisa dividir pelo logaritmo da nova base.
Agora, se você tem uma orientação artística, pode desfrutar da forma alternativa da fórmula de mudança de base expressa abaixo:
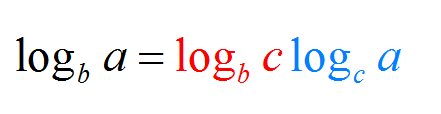
EXEMPLO 3
Expresse o log natural \(\ln\) em termos de \(\log\) (base 10).
RESPONDA:
Usando a mudança da fórmula de base, obtemos que:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]Então você está dizendo que \(\ln a\) é imprimir dividindo \(\log a\) por \(\log e\). Quão conveniente? Quem disse que matemática era difícil, hein?
Mais sobre as regras de registro
Logaritmos são muito importantes em matemática. Historicamente, os logaritmos desempenham um papel muito importante na Astronomia, como forma de prever o movimento da lua e dos planetas.
As funções logarítmicas estão no meio de tudo no Math, e se entrelaçam com exponenciais, expoentes e quase tudo. É por isso que eles pedem que você aprenda os logaritmos de cor, porque eles são importantes.
Além disso, essas regras de registro aqui desempenham um papel crucial em facilitar o resolução de equações logarítmicas .
Convenções de notação
Existem algumas convenções de notação que você precisa conhecer. Em geral, escrevemos \(\log_b a\) e dizemos "log base b de a". Quando a base é \(b = 10\), por convençãoemos apenas \(\log a\). Portanto, quando você vê um \(\log\) sem uma base, assume-se que uma base é \(10\).
Existe outro caso notável. Para \(\log_b a\), quando a base é \(b = e\) (a constante de Euler), então escrevemos \(\ln a\) em vez de \(\log_e a\). Portanto, quando \(\ln\) é usado em vez de \(\log\), é porque uma base do logaritmo é \(e\).
Observe que \(\ln a\) é comummente como o tronco natural . E sim, os logs naturais têm as mesmas regras que o log geral.
Se você tem uma função logarítmica que gostaria de representar graficamente, pode tentar nosso Criador de gráficos de funções logarítmicas , que fornecerá um gráfico bem apresentado.
