Operações com expoentes negativos
As operações com expoentes estão entre as operações mais fundamentais em Álgebra e, entre elas, as que envolvem expoentes negativos são as que mais complicam os alunos.
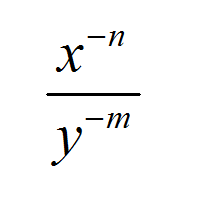
Primeiro, vamos relembrar as propriedades básicas do expoente. O uso dessas propriedades é onipresente na maioria das áreas da matemática. As regras são:
Regra 1: \(\large \displaystyle x^0 = 1\), para \(x = \not 0\)
Regra 2: \(\large\displaystyle x^1 = x\)
Regra 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Regra 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Regra 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Por exemplo, quando você tem uma expressão como \(3^5 \cdot 3^7\), sabemos que usamos a regra de multiplicação (Regra 3) para obter:
\[\large 3^5 \cdot 3^7 = 3^{5+7} = 3^{12}\]As regras do expoente: o que acontece com os expoentes negativos?
Mesmo que você não tenha percebido, as regras acima não dizem que os expoentes precisam ser positivos. Na verdade, eles podem ser negativos e as regras também serão válidas.
Agora, das Regras 1 e 5, podemos derivar a relação entre expoentes positivos e negativos. Portanto, para a Regra 5, assuma que \(m = 0\) e \(n\) são positivos. Então, nós temos
\[\large\displaystyle \frac{1}{x^n} = \frac{x^0}{x^n} = x^{0-n} = x^{-n}\]A expressão acima nos dá uma relação simples entre expoentes positivos e negativos:
\[\large\displaystyle \boxed{\frac{1}{x^n} = x^{-n}}\]
A expressão acima está nos dizendo que podemos passar uma potência com um expoente negativo no numerador para o denominador com o expoente positivo correspondente. Esta é uma 'regra' de expoentes negativos
A beleza da fórmula acima é que podemos cruzar e multiplicar os termos em ambos os lados da igualdade, e podemos escrever a expressão acima de uma forma ligeiramente diferente:
\[\large\displaystyle \boxed{\frac{1}{x^{-n}} = x^{n}}\]
Esta última expressão é geralmente muito útil, porque nos diz que podemos trazer uma potência com expoente negativo no denominador para o numerador, mas com o expoente positivo correspondente. Isso pode ser considerado como outra "regra" para expoentes negativos.
EXEMPLO 1
Simplifique a seguinte expressão e deixe sem expoentes negativos:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2}\]RESPONDA:
Usando a regra de expoentes negativos, trocamos expoentes positivos / negativos entre numerador / denominador:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2} = \frac{x^{3}\sqrt{x} x^{1/2}}{ y^2 y^{3}}\] \[\large = \frac{x^{3} x^{1/2} x^{1/2}}{ y^2 y^3} = \frac{x^{3+1/2+1/2}}{ y^{2+3}} \] \[\large = \frac{x^{4}}{ y^{5}} \]e terminamos a simplificação, porque não há mais nada para simplificar.
Mais sobre expoentes negativos
Uma das maiores lições deste tutorial sobre expoentes negativos é que temos regras para transformar esses expoentes negativos em expoentes positivos. Como fazemos isso?
• Se tivermos um expoente negativo no numerador (então você está multiplicando por um expoente negativo), podemos passá-lo para o denominador com expoente positivo.
• Se tivermos um expoente negativo no denominador (então você está dividindo por um expoente negativo), podemos passá-lo para o numerador com expoente positivo.
Operar com expoentes negativos é apenas uma pequena parte do tópico de lidar com regras de expoentes , que fornecem uma visão clara de por que o caso com expoentes negativos funciona da maneira que funciona.