O gráfico de uma função é um conjunto de pares ordenados \((x,y)\). Ou, o gráfico de uma função é uma conceituação que fazemos um conjunto de pares \((x,y)\) em um sistema de coordenadas. Eu digo que é uma conceituação, porque a maneira como representamos um gráfico é, até certo ponto, uma ilusão de ótica.

Por que eu digo isso? Bem, dê uma olhada. O que você pensa quando digo "gráfico". Verifique a figura antes.

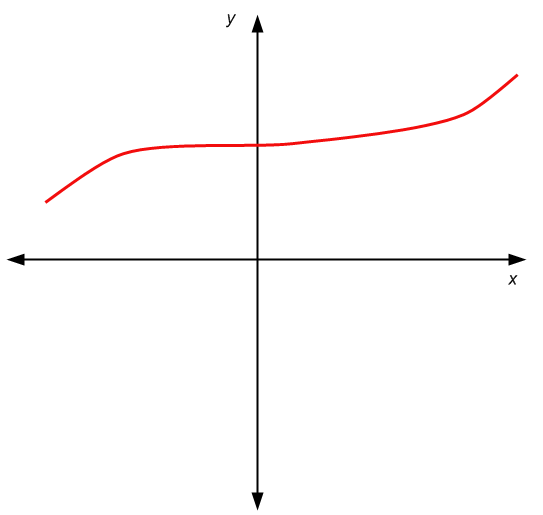
Então esse é um gráfico. Um conjunto de pares \((x, y)\), ou como também podemos chamá-los, pontos. Um ponto específico é destacado abaixo, dê uma olhada

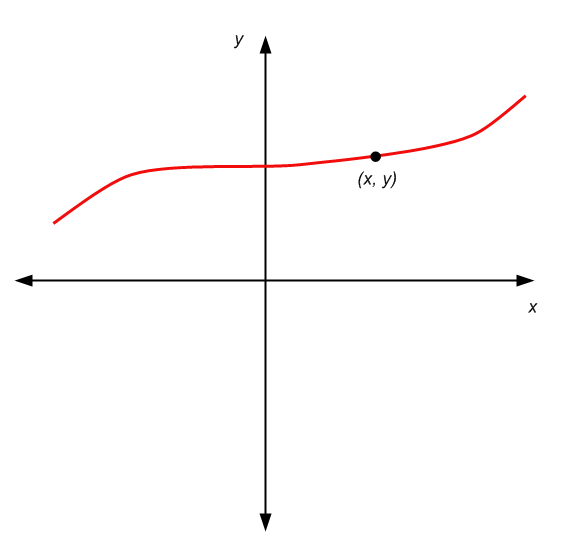
O truque, ou a ilusão visual, é que um ponto não tem, em teoria, dimensões (sem largura, sem comprimento). Então, essa "curva" que desenhamos para representar um gráfico, é uma forma conveniente de representar um gráfico, mas estamos meio que trapaceando, porque essa representação tem uma curva que tem uma espessura.

Então, isso não é para chover no seu desfile, é apenas para deixar claro que o que você entende por gráfico, é antes um representação de um gráfico que seja conveniente e confiável.

Gráficos associados a funções

Uma maneira realmente fácil de definir um gráfico é usando a função \(f(x)\). De fato, um gráfico definido por uma função \(f(x)\) é o conjunto de todos os pontos \((x, f(x))\), para \(x \in D\), onde \(D\) é o domínio da função \(f\).

A representação é a mesma dos gráficos anteriores, só que agora fazemos o seguinte:

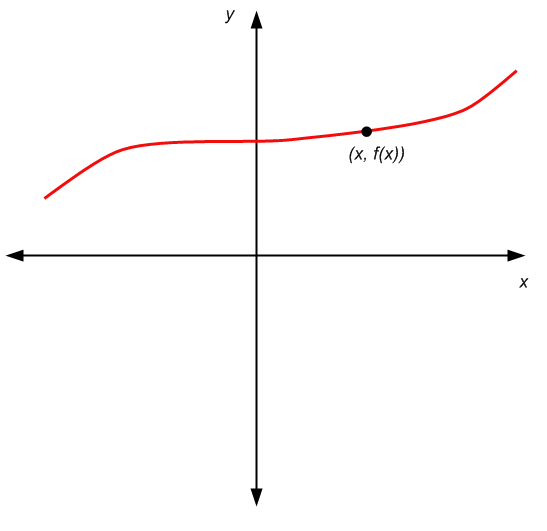
Nesse caso, a diferença mais clara é que o segundo componente do par \((x,y)\) não é qualquer valor \(y\). O segundo componente é \(f(x)\), portanto, é determinado exclusivamente por \(x\).

EXEMPLO 1

Trace o gráfico da função \(f(x) = x^2\).

RESPONDA:

Nada de estranho, só precisa desenhar o gráfico de uma função. Os pontos no gráfico têm o formato \((x, f(x)) = (x, x^2)\). Ou seja, o valor de \(x\) está associado a \(x^2\) no gráfico.

Exemplos de pontos que estão no gráfico: \((1, 1)\), \((2, 2^2) = (2, 4)\), \((3, 3^2) = (3, 9)\), etc. Graficamente, obtemos a seguinte representação do gráfico:

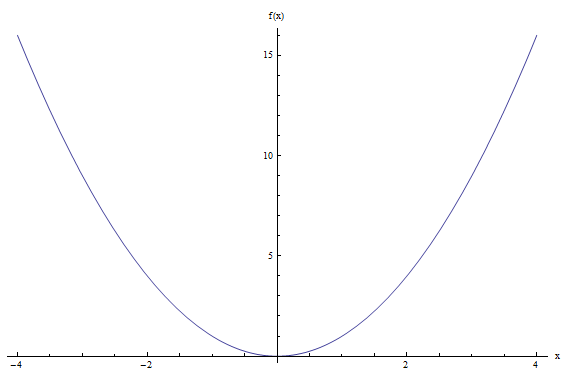
Gráficos contínuos versus descontínuos

Uma das suposições que fazemos em nossas mentes quando pensamos em um gráfico é que é suave, sem saltos. Esse não é sempre o caso. Existem funções que levam a funções que saltam, ou mesmo levam a gráficos estranhos. Outras funções têm gráficos muito suaves, como aconteceu com \(f(x) = x^2\).

O conceito de suavidade de uma função é tratado formalmente no Cálculo, com a noção de função contínua. Mas sem muito fuzz, podemos dizer que, por enquanto, vamos pensar que uma função contínua é uma função que tem um gráfico "suave", e uma função descontínua é uma função que não é suave, ou que tem "saltos"

EXEMPLO 2

A função \(f(x) = sin(x)\) é contínua?

RESPONDA:

Bem, novamente, precisaríamos de uma análise de continuidade formal para verificar. Mas à luz da definição informal dada acima, vamos verificar seu gráfico. O computador nos dá o seguinte:

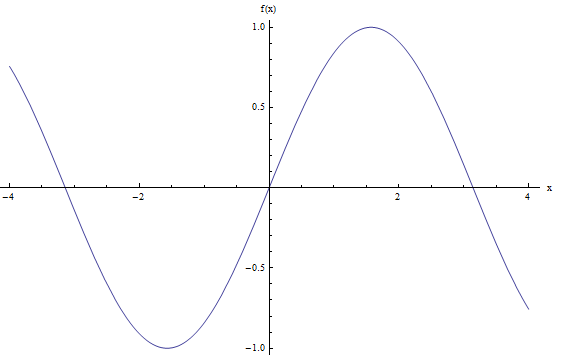
Eu diria que o gráfico acima parece muito bom, sem saltos, então usando nossa definição ingênua, eu diria que \(f(x) = \sin x\) é contínuo.

EXEMPLO 3

A função \( f\left( x \right)=\left\{ \begin{array}{cc}-1 &\,\,\,\,\text{for } x\le 1 \\ \\ x & \,\,\,\,\,\,\text{for }x>1 \\ \end{array} \right.\) é contínua?

RESPONDA:

Para responder à pergunta, precisamos traçar o gráfico. O computador nos dá o seguinte:

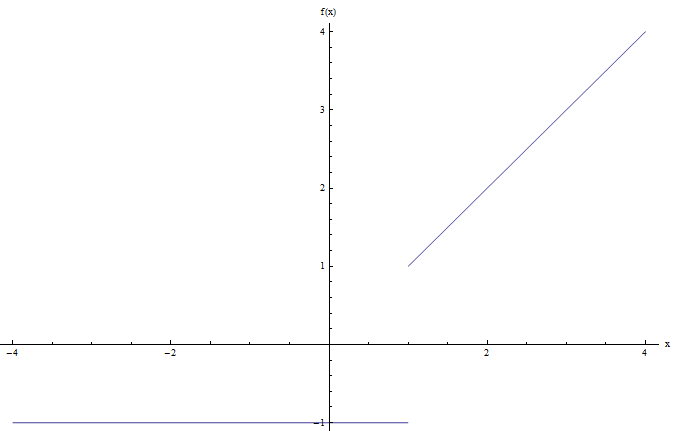
Observe que há um salto no ponto \(x = 1\), então eu diria que o gráfico acima tem um salto e, portanto, esta função é descontínua.

Mais sobre gráficos

O uso de gráficos para fazer uma representação de uma função pode ser um papel crucial para a compreensão do comportamento de uma função.

Existem ferramentas analíticas (Cálculo) suficientes para entender o comportamento de uma função \(f(x)\), sem a necessidade de traçá-la. Porém, é muito prático ver um gráfico porque é uma maneira muito rápida de se ter uma ideia do que a função está fazendo.

Observe que nem todos os gráficos devem vir de funções. Por exemplo, os gráficos também podem vir de relações. Veja o gráfico abaixo e diga-me se conseguir descobrir que relação está associada a ele.

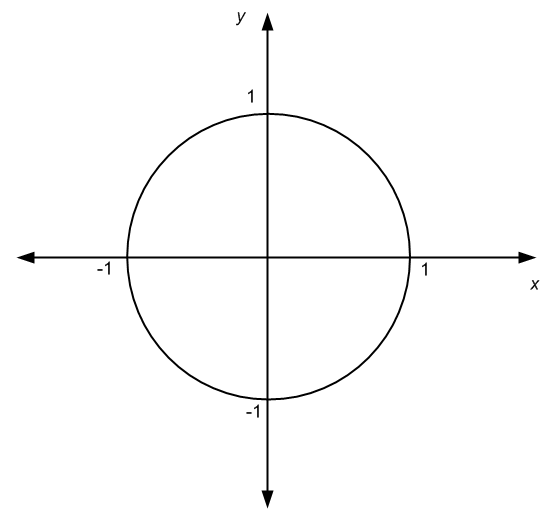
Você acertou, aquele gráfico acima é uma representação da equação de um círculo unitário, \(x^2 + y^2 = 1\), que como já sabemos, ele determina uma relação, e não uma função.

Se você precisa construir um gráfico, experimente gráfico de função para obter uma boa descrição de como uma função se comporta.