Calculadora de Matriz Determinante
Instruções: Utilize esta calculadora do determinante da matriz, para calcular o determinado determinante de uma matriz, mostrando todos os passos. Primeiro, clique num dos botões abaixo para alterar a dimensão da matriz, se necessário.
Depois, clicar na primeira célula e digitar o valor, e mover-se em torno da matriz pressionando "TAB" ou clicando nas células correspondentes, para definir TODOS os valores da matriz.
Mais sobre esta calculadora determinante.
Na álgebra linear e na utilização de matrizes, a ideia do determinante de uma matriz \(A\) é um conceito da mais profunda importância.
Isto porque a sua utilização está ligada a quase todas as operações significativas que desejará fazer com matrizes, tais como a verificação da invertibilidade das matrizes, encontrar o inverso de uma matriz ou sistemas de resolução .
Assim, onde quer que olhe à sua volta quando trabalha com matrizes, encontrará determinantes de uma forma ou de outra. Portanto, é muito importante familiarizar-se com eles.
Como é que esta calculadora matricial o pode ajudar
- Tudo o que precisa de fazer é digitar a sua matriz
- Tem de ser uma matriz quadrada, isto é, uma matriz com o mesmo número de filas e colunas
- Basta clicar no botão e a calculadora mostrar-lhe-á todos os passos e o valor final do determinante
- Trabalhar em cálculos determinantes pode ser extremamente trabalhoso e propenso a erros. Esta calculadora poupa-o a esses problemas
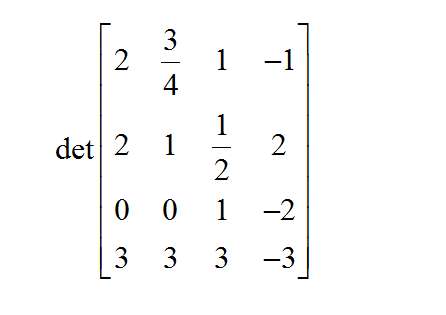
Como se calcula o factor determinante de uma matriz?
Isso poderia ser uma resposta longa, porque há muitas maneiras de calcular o determinante de uma matriz. Digamos primeiro que os determinantes são apenas cálculos para matrizes quadradas (isto é matrizes que têm o mesmo número de filas e colunas).
Assim, a menor matriz para a qual podemos calcular um determinante é uma matriz 2x2. Consideremos uma matriz genérica de 2x2, como se mostra abaixo:
\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]Qual é a fórmula do determinante? Neste caso, o determinante da matriz \(A\) é simplesmente calculado como \(\det(A) = a d - bc\)>
Assim, por exemplo, se o tivéssemos feito:
\[ A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\]o determinante da matriz <\(A\) seria \(\det(A) = 1 \cdot 3 - 2 \cdot 1 = 3 - 2 = 1\)>>. Fácil, certo?
Como se encontra o determinante de uma matriz 3x3?
Agora, para matrizes maiores, construímos o cálculo do determinante com base no sub-determinante de matrizes mais pequenas. Só para lhe dar um sabor, vamos ver uma forma de calcular o determinante de uma matriz 3x3. Considere
\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]Neste caso, o determinante da matriz 3x3 matriz \(A\) é calculado com base na operação de vários determinantes 2x2
\[\det(A) = a \det \begin{bmatrix}e & f \\ h & i \end{bmatrix} - b \det \begin{bmatrix} d & f \\ g & i \end{bmatrix} + c \det\begin{bmatrix} d & e \\ g & h \end{bmatrix}\]Nas equações acima, os valores \(a\), \(b\), \(c\) desempenham o papel de pivôs, e podem obter um sinal negativo. O sinal de um pivô é <\((-1)^{i+j}\), onde o pivô correspondente está na fila \(i\) e na coluna \(j\)>>.
Por exemplo <\(a\) está na linha 1, coluna 1, portanto o seu sinal é \((-1)^{1+1} = (-1)^2 = 1\)> (positivo). Também, <\(b\) está na fila 1, coluna 2, pelo que o seu signo é \((-1)^{1+2} = (-1)^3 = -1\) (negativo), e assim por diante.
A magia é escolher qualquer linha ou coluna como pivots. Cada pivô terá um sinal associado (positivo ou negativo) e um sub-determinante, que estão relacionados com a co-factores de matriz .
Este sub-determinante é o verdadeiro determinante da matriz original após a remoção da linha \(i\) e coluna \(j\), para pivot que está na linha \(i\) e coluna \(j\)>.
A convenção mais lógica indica a escolha da fila ou colum com mais zeros para os pivots, de modo a evitar calcular alguns dos sub-determinantes, se possível.
Como é que se encontra o determinante de uma matriz 3x4?
Não o pode fazer. Uma matriz 3x4 não é uma matriz quadrada, e por isso, nenhum determinante pode ser computado. Para calcular um determinante, a matriz precisa de ter o mesmo número de filas e colunas.
Uma calculadora 4x4 determinante
Para matrizes maiores, a metodologia é a mesma: Escolha uma linha ou coluna para os pivôs, idealmente aquela com o maior número de zeros. Encontrar o sinal correspondente a cada pivô, e encontrar os sub-determinantes correspondentes.
Assim, reduz-se o cálculo do determinante de uma matriz 4x4 para a operação de quatro determinantes 3x3. E, por sua vez, cada um dos determinantes 3x3 é encontrado como a operação de vários determinantes 2x2, para os quais conhecemos uma fórmula.
Por isso, pode ficar desarrumado muito rapidamente.

Exemplo de cálculo de um determinante de matriz
Pergunta: Considere a seguinte matriz:
\[ \begin{bmatrix}1&2&3\\3&1&4\\2&3&8\end{bmatrix}\]Calcular o factor determinante da matriz dada, mostrando os passos.
Solução: Precisamos de calcular o determinante da matriz \(3 \times 3\) que foi fornecida.
Usando a fórmula sub-determinante que obtemos:
\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 3&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 8 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 8 \right) - 3 \cdot \left(4 \right) \right) - 2 \cdot \left( 3 \cdot \left( 8 \right) - 2 \cdot \left(4 \right) \right) + 3 \cdot \left( 3 \cdot \left( 3 \right) - 2 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -4 \right) - 2 \cdot \left( 16 \right) + 3 \cdot \left( 7 \right) = -15\]Conclusão : Com base nos cálculos apresentados acima, verifica-se que o determinante da matriz é \(\det A = \displaystyle -15\)>>.
Outras calculadoras matriciais úteis que pode utilizar
Os cálculos de matriz feitos à mão são trabalhosos, pelo que pode tirar partido dos nossos solucionadores de álgebra linear.
Primeiro, pode usar esta calculadora de matriz inversa para calcular o inverso de uma matriz mostrando passos, e pode fazê-lo por método em anexo , ou utilizando Redução de RREF .