Calculadora do Sistema de Equações para Matriz
Instruções: Use esta calculadora para encontrar a representação matricial de um determinado sistema de equações que você fornece. Por favor, especifique um sistema de equação linear, ajustando primeiro a dimensão, se necessário.
Em seguida, preencha os coeficientes associados a todas as variáveis e o tamanho à direita, para cada uma das equações. Se uma variável não estiver presente em uma equação específica, digite "0" ou deixe em branco.
Mais sobre este sistema de equações para a calculadora de forma matricial
Uma habilidade crucial quando Resolvendo sistemas de equações lineares é poder passar do formato tradicional de sistemas lineares para matrizes.
Um você tem a representação matricial de um sistema linear, então você pode aplicar Regra de Cramer ou você pode resolver o sistema primeiro encontrando o inverso da matriz de coeficientes correspondente.
Ou, com a representação da matriz, você pode construir a matriz aumentada e conduzir o método de pivotagem de Gauss, o que melhor lhe convier.
Primeiro: Como você escreve um sistema de equações na forma matricial?
Passo 1: Identifique cada uma das equações do sistema. Cada equação corresponderá a uma linha na representação matricial.
Passo 2: Vá trabalhando em cada equação. Para cada um deles, identifique o lado esquerdo e o lado direito da equação.
Passo 3: O que estiver do lado esquerdo fará parte da matriz A, e o que estiver do lado direito fará parte do vetor b
Passo 4: Os coeficientes à esquerda precisam ser identificados separadamente em função de qual coeficiente multiplica cada variável.
Etapa 5: Cada equação representa uma linha e cada variável representa uma coluna da matriz A.
Como você usa uma matriz para resolver um sistema de equações?
Uma vez que você tenha um sistema em forma de matriz, há várias maneiras de resolver o sistema. Normalmente, você começa primeiro com computação do determinante da matriz , como critério inicial para conhecer as soluções do sistema.
Quando \(\det A \ne 0\), então sabemos que o sistema tem uma solução única. Agora, quando \(\det A = 0\), isso não significa que você não tem soluções, significa apenas que se existem soluções, não é único.
De fato, quando \(\det A = 0\), você não pode usar Método de Cramer ou o método inverso para resolva o sistema de equações . Nesse caso, é melhor usar o método pivotante de Gauss.
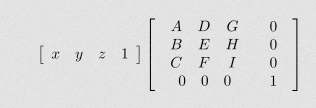
Como resolver equações matriciais
Muitas vezes, você recebe um sistema de equações diretamente no formato de matriz. Se for esse o caso, e o número de equações for igual ao número de variáveis, você pode tentar usar o método inverso ou a Regra de Cramer. Caso contrário, você pode usar o método de Gauss.
Agora, você pode usar esta calculadora para expressar um sistema em uma forma tradicional quando dada uma forma matricial.



