Aprender como fatorar é uma das habilidades mais importantes que você pode aprender. O fatoração tem tantas aplicações, que você ficará feliz em dedicar um tempo para aprender tudo o que há sobre ele.

Uma rápida atualização sobre a propriedade comutativa, associativa e distributiva. Para os números reais \(x\), \(y\) e \(z\), temos as seguintes propriedades

(Associatividade de adição) \((x+y)+z = x+(y+z)\)

Comutatividade de adição) \( x + y = y + x\)

(Propriedade distributiva) \( x \cdot (y+z) = x \cdot y + x \cdot z\)

onde \(+\) e \(\cdot\) são a soma e o produto dos números reais, respectivamente.

Por que é útil saber como fatorar?

Existem muitas razões, mas uma das principais é que a fatoração nos dá uma maneira fácil de resolver equações. Na verdade, a fatoração é A maneira que temos de resolver equações.

Por exemplo, considere a equação em que estamos tentando resolver para \(x\):

Como vamos fazer isso? Bem, podemos usar a propriedade distributiva para obter:

Portanto, com esta última expressão \( x(y+z) = 0\) temos um exemplo de fatoração. Na verdade, pegamos a expressão inicial, \(xy+xz\) e a fatoramos em \( x(y+z)\).

Então, agora precisamos resolver uma equação mais fácil, que é \( x(y+z) = 0\). Por que é mais fácil? É porque agora que sabemos que o produto \( x(y+z)\) é igual a zero, então um dos fatores PRECISA ser igual a zero.

Portanto, se sabemos que \(y+z = \not 0\), então sabemos que precisamos ter esse \(x = 0\).

LIÇÃO : Uma vantagem da fatoração é ser capaz de escrever uma equação como uma multiplicação de fatores que é igual a zero. Então, PELO MENOS UM DOS FATORES DEVE SER ZERO.

Por exemplo, quando precisamos resolver para \(x\) na seguinte equação:

não percebemos que estamos fatorando quando fazemos

portanto, reduzimos nossa equação a um produto de fatores igual a zero: \(8x = 0\). Como um dos fatores \(8\) não é igual a zero, então a única solução possível é \(x = 0\).

Em outras palavras : se você souber como fatorar, provavelmente saberá como resolver equações .

Como fatorar polinômios

O equilíbrio é alcançado com uma classe muito geral de expressões que podemos, muitas vezes, fatorar de forma muito sistemática. Essa classe é a classe dos polinômios. Por exemplo, a expressão

é um polinômio de grau 2. Ou a expressão abaixo

é um polinômio de grau 3.

Em geral, uma expressão do formulário

é um polinômio de grau \(n\). Naturalmente, quanto mais simples for a expressão, mais fácil será simplificá-la, portanto, devemos tentar aprender como fatorar expressões quadráticas primeiro. Isto é, polinômios de grau dois.

EXEMPLO 1

Fatore a seguinte expressão quadrática

RESPONDA:

Este exemplo irá mostrar a você, propositalmente, que pode ser complicado fatorar até mesmo a expressão mais simples, como a acima. O que você faria para fatorá-lo?

E se eu disser que você precisa adicionar zero? É meio ridículo, certo? Vamos ver:

Você concorda com o acima? Acabei de adicionar \(0\). Nada mudou. Mas, e se eu te contar isso \(0 = 2x - 2x\)? Então

Tudo o mesmo! Funciona, porque adicionei zero, então nada muda. Mas agora vamos expandi-lo e agrupá-lo:

Então, finalmente, \(x^2 + x - 2 = (x+2)(x-1)\). Complicado? Talvez, mas essa é uma maneira de fazer isso. Apesar de ser uma maneira inteligente de fazer isso, preferiríamos uma forma mais sistemática.

Fator um polinômio quadrático

Truques inteligentes são legais e tudo isso, mas geralmente preferimos uma abordagem sistemática, que nunca falha. Para polinômios quadráticos (polinômios de grau 2), existe uma forma sistemática de proceder com a fatoração:

Passo 1 : Dada a expressão quadrática \(ax^2 + bx + c\), primeiro resolvemos a equação

Passo 2 : Se as soluções (raízes) para a equação acima forem reais (mesmo se houver apenas uma raiz), chamamos essas raízes de \(x_1\) e \(x_2\). Com essas raízes, obtemos os seguintes fatores:

assim, as soluções \(x_1\) e \(x_2\) determinam completamente os fatores.

Naturalmente, neste caso, como esperado, a resolução de uma equação quadrática está intimamente ligada à fatoração da equação quadrática.

EXEMPLO 2

Fatore a seguinte equação quadrática

calculando suas raízes.

RESPONDA:

Começamos resolvendo a equação quadrática correspondente:

usando o famoso e bem conhecido Fórmula quadrática :

o que implica que as soluções (raízes) são \(x_1 = 1\) e \(x_2 = 1\). Então, a expressão quadrática \(x^2 - 4x + 3\) pode ser fatorada da seguinte maneira:

Observe que neste caso o termo que multiplica o termo \(x^2\) é 1, então neste caso \(a = 1\).

Fatoração de polinômios com grau maior que 2

Então, para fatorar polinômios quadráticos, eu apenas calculo as raízes da equação quadrática correspondente. Como faço para fatorar polinômios de alto grau ?? Usando exatamente o mesmo método .

Passo 1: Dada a expressão polinomial \(a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\), primeiro resolvemos a equação

Passo 2: Se as soluções (raízes) para a equação acima forem reais (mesmo se forem repetidas), chamamos essas raízes de \(x_1\), \(x_2\), ..., \(x_n\). Com essas raízes, obtemos os seguintes fatores:

Portanto, parece que é tão simples fatorar um polinômio de grau 2 quanto fatorar um polinômio de grau 10. Teoricamente, a resposta é sim.

O único problema é que não existe uma fórmula algébrica simples e próxima que possa resolver as raízes de uma equação polinomial de grau 5 ou superior.

Às vezes, podemos resolver equações de grau superior olhando para o gráfico ou mesmo usando a calculadora. Por exemplo, verifique o gráfico abaixo:

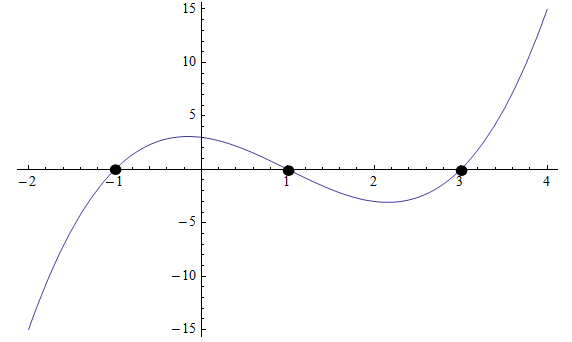
Graficamente, podemos ver que o polinômio cruza o eixo x em três pontos: \(x_1 = -1\), \(x_2 = 1\) e \(x_3 = 3\), então essas são as raízes.

Então, sabemos que o polinômio deve estar no formato \(p(x) = a(x+1)(x-1)(x-3)\). Precisaríamos saber mais um ponto para saber a constante \(a\).