Calculadora de coeficiente de correlação

O coeficiente de correlação calculado acima corresponde ao coeficiente de correlação de Pearson. Os requisitos para calculá-lo é que as duas variáveis X e Y sejam medidas pelo menos no nível do intervalo (o que significa que não funciona com variáveis nominais ou ordinais).

A fórmula para o coeficiente de correlação de Pearson é:

\[r =\frac{n \sum_{i=1}^n x_i y_i - \left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{n \sum_{i=1}^n x_i^2 - \left( \sum_{i=1}^n x_i \right)^2} \sqrt{n \sum_{i=1}^n y_i^2 - \left( \sum_{i=1}^n y_i \right)^2} }\]

ou equivalente

\[r = \frac{\sum_{i=1}^n x_i y_i - \frac{1}{n}\left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{\sum_{i=1}^n x_i^2 - \frac{1}{n}\left( \sum_{i=1}^n x_i \right)^2} \sqrt{\sum_{i=1}^n y_i^2 - \frac{1}{n}\left( \sum_{i=1}^n y_i \right)^2}} = \frac{SS_{XY}}{\sqrt{SS_{XX}\cdot SS_{YY} }}\]

Se você tiver duas ou mais variáveis, você pode usar nosso calculadora de matriz de correlação . Além disso, se os dados das variáveis \(X\) e \(Y\) não atendem às suposições paramétricas da correlação de Pearson, você deve usar este Calculadora de correlação de Spearman em vez de.

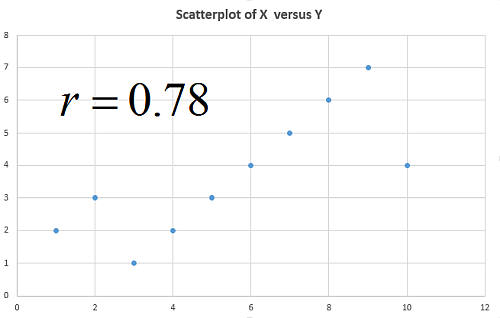
Correlação e regressão

Correlação e regressão não são a mesma coisa, embora sejam conceitos intimamente relacionados. A análise de correlação corresponde ao cálculo do coeficiente de correlação, que é um valor que varia de -1 a 1, que avalia o grau de associação linear entre duas variáveis.

Quanto mais próximo em valor absoluto correlação chega a 1, mais estreita é a associação linear entre as duas variáveis. Perto de 1 indica uma associação linear positiva forte e perto de -1 indica uma associação negativa forte

O processo de conduzir uma análise de correlação muitas vezes também envolve construindo um gráfico de dispersão , a fim de confirmar a informação fornecida pelo coeficiente do coeficiente.

Depois de confirmarmos que a correlação está próxima de 1 em valor absoluto e que o gráfico de dispersão mostra um padrão linear razoavelmente rígido, podemos executar um Regressão linear análise, a fim de avaliar quantitativamente o efeito da variável independente X na variável dependente Y.

Posso usar escores z para calcular o coeficiente de correlação

Certamente! Você já viu z-scores em toda parte em Estatística e, naturalmente, você se pergunta se pode calcular a correlação com os escores z . Você pode definitivamente fazer isso e, de fato, é a maneira usual de fazê-lo nas estatísticas de Ciências Sociais.

Outras calculadoras semelhantes a esta calculadora de correlação

Além disso, existe o conceito de coeficiente de correlação múltipla , quando você tem mais de um preditor, que é obtido calculando a correlação entre os valores \(Y\) observados e os valores preditos \(\hat Y\) pela regressão.