Álgebra Tutoriais

A hipérbole

Uma hipérbole é o lugar geométrico dos pontos nos eixos coordenados que têm a propriedade de que a diferença entre as distâncias a dois pontos fixos (os focos), é igual a uma constante, que denominamos $2a$ .

Naturalmente, isso soa um pouco intimidante e muito técnico, mas é realmente a forma como uma hipérbole é definida.

Talvez, se eu der a equação de uma hipérbole, você a "reconheça".

Vamos tentar: esta é a equação de uma hipérbole muito geral:

\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1

Você poderia descobrir como fica apenas verificando sua equação? Provavelmente não. Então, eu apresento a hipérbole, graficamente para você:

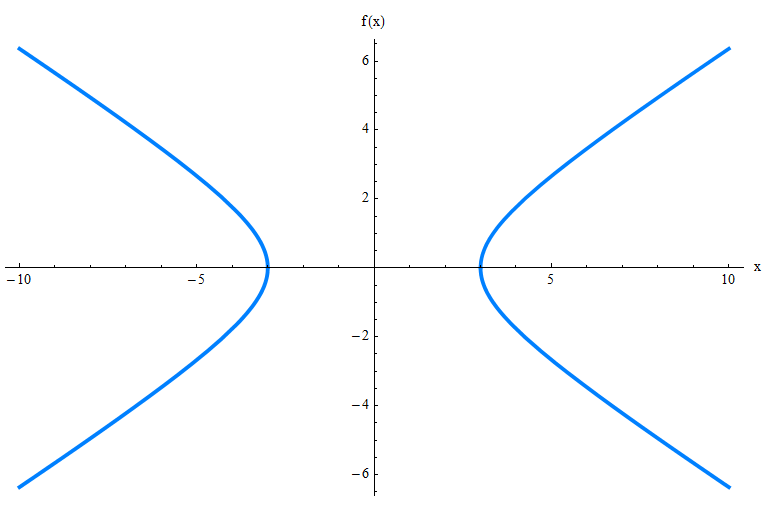
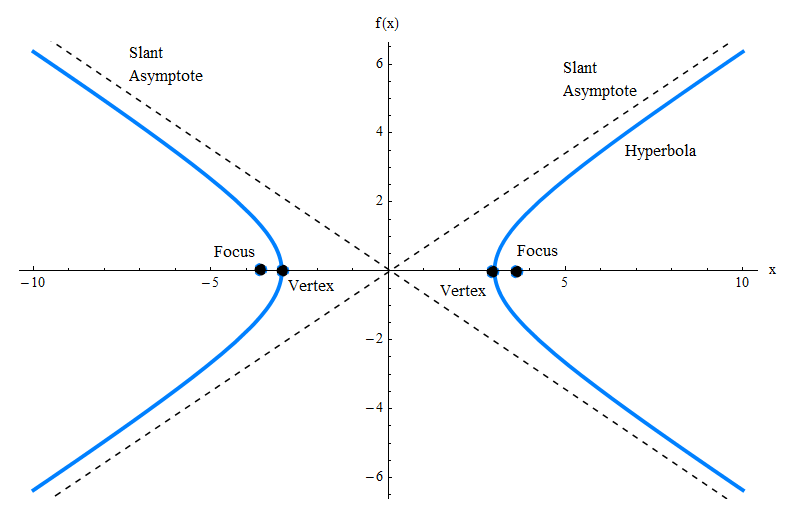
O gráfico acima mostra apenas o gráfico da hipérbole, mas existem muitos outros elementos dos quais você precisa estar ciente, como as assíntotas inclinadas, os vértices e os focos. Confira o gráfico abaixo.

Hipérbole com seus focos, vértices e assíntotas oblíquas

A Equação Geral da Hipérbole

Sem muita discussão teórica, afirmaremos que a equação geral da hipérbole com focos no eixo x é

\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1

Para a hipérbole descrita pela equação acima, ela possui vértices nos pontos $(-a, 0)$ e $(a, 0)$ e focos nos pontos $(-c, 0)$ e $(c, 0)$ , onde $c = \sqrt{a^2 + b^2}$ .

Uma característica interessante dessa hipérbole é que ela tem duas assíntotas inclinadas

Assíntota 1 : $\displaystyle y = \frac{b}{a}x$

Assíntota 2 : $\displaystyle y = -\frac{b}{a}x$

Agora, o que acontece com a equação da hipérbole, se em vez disso os vértices são traduzidos por um determinado ponto $(k,h)$ ?

Nesse caso, tudo que você precisa fazer é substituir $x$ por $x-k$ e substituir $y$ por $x-h$ .

Portanto, ao fazer uma tradução, obtemos que a equação de uma hipérbole geral é

\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} - \frac{(y-h)^2}{b^2} = 1 }

A hipérbole acima possui vértices nos pontos $(k-a, h)$ e $(k+a, h)$ e focos nos pontos $(k-c, h)$ e $(k+c, h)$ , onde $c = \sqrt{a^2 + b^2}$ .

As equações das assíntotas inclinadas são $y = \frac{b}{a}(x-k) + h$ e $y = -\frac{b}{a}(x-k) + h$ .

O que acontece com as hipérboles que se abrem ao longo do eixo y?

Por simetria, tudo o que temos a fazer é simplesmente substituir os papéis de $x$ e $y$ na equação geral da hipérbole que já temos. Na prática, isso significa que onde quer que $x$ apareça na equação da parábola que temos, nós o trocamos $y$ , e vice-versa por $y$ .

Então, no caso de uma hipérbole que abre ao longo do eixo x, a equação geral é

\large \boxed{\displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 }

A hipérbole acima possui vértices nos pontos $(k, h - b)$ e $(k, h+b$ e focos nos pontos $(k, h-c)$ e $(k, h+c)$ , onde $c = \sqrt{a^2 + b^2}$ .

As equações das assíntotas inclinadas são $y = \frac{b}{a}(x-k) + h$ e $y = -\frac{b}{a}(x-k) + h$ .

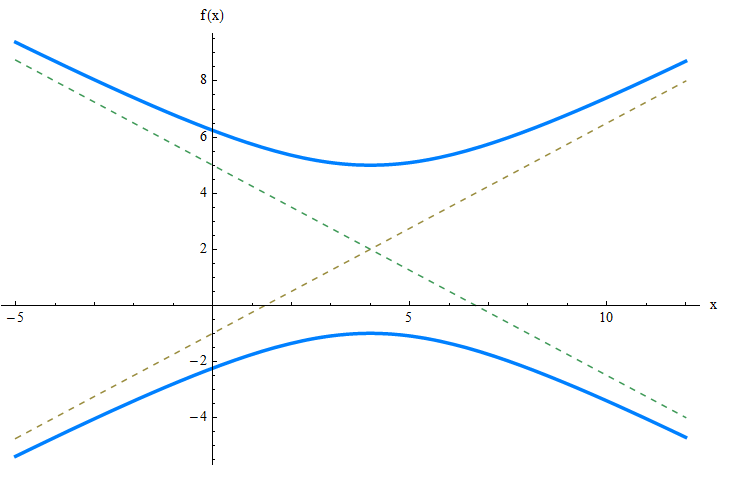
EXEMPLO 1

Encontre os focos, vértices e assíntotas oblíquas da hipérbole:

\large \displaystyle \frac{(y-2)^2}{9} - \frac{(x-4)^2}{16} = 1

RESPONDA:

Essa hipérbole se abre ao longo do eixo y. Neste caso, os valores de tradução são $k = 4$ e $h = 2$ . Além disso, obtemos $a = \sqrt{16} = 4$ e $b = \sqrt{9} = 3$ . Portanto, obtemos esse $c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5$ .

Portanto, os focos são $(k, h-c) = (4, 2 - 5) = (4, -3)$ e $(k, h+c) = (4, 2 + 5) = (4, 7)$ .

Os vértices são $(k, h-b) = (4, 2 - 3) = (4, -1)$ e $(k, h+b) = (4, 2 + 3) = (4, 5)$ .

As assíntotas inclinadas são

\displaystyle y = \frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2

\displaystyle y = -\frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2

Graficamente:

EXEMPLO 2

Encontre a equação da hipérbole com focos no vértice $(-4, 0)$ e $(4, 0)$ , foco em $(6, 0$ .

RESPONDA:

Observe que os focos e vértices estão no eixo x, então a hipérbole se abre ao longo do eixo x. Além disso, como os focos são simétricos em relação à origem, e um vértice é $(4, 0)$ , obtemos esse $a = 4$ . E como um dos focos está em $(6, 0)$ , obtemos esse $b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5$ .

Portanto, a equação da hipérbole é:

\large \displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1

\large \displaystyle \Rightarrow \frac{x^2}{16} - \frac{y^2}{20} = 1

A hipérbole e as seções cônicas gerais

Da mesma forma que no caso da parábola, a hipérbole está intimamente relacionada ao cone. Na verdade, um matemático grego chamado Apolônio é quem descobriu essa conexão, ao compreender o conceito de seções cônicas.

Uma seção cônica ocorre quando você faz um corte de um cone com um plano e, dependendo do ângulo relativo do cone e do plano no ponto de corte, o cone é cortado de uma forma em que a seção transversal tenha uma forma específica .

Portanto, dependendo do ângulo de corte relativo, temos diferentes formas de seção, e essas são a parábola, o círculo, a elipse e a hipérbole. Veja o gráfico abaixo:

Mais sobre a hipérbole

Uma hipérbole com vértice na origem, que abre ao longo do eixo x tem a equação $\displaystyle \frac{x^2}{a^2} - \frac{y^2}{a^2} = 1$ , enquanto uma hipérbole, que se abre ao longo do eixo y tem a equação $\displaystyle \frac{y^2}{a^2} - \frac{x^2}{a^2} = 1$ .

Então, um vértice geral pode ser obtido simplesmente aplicando uma translação a um determinado ponto $(k, h)$ .

Formulários

A hipérbole tem muitas aplicações no mundo prático, bem como na Astronomia. Uma diferença com a parábola é que a hipérbole tem assíntotas inclinadas, o que a parábola não possui.

Falando algebricamente, uma hipérbole se parece muito mais com uma elipse do que com uma parábola, embora a diferença de sinal com a elipse faça um mundo de diferença em sua forma e propriedades.

Outro tipo importante de seção cônica é a parábola, da qual você pode aprender neste tutorial . Além disso, você também pode aprender tudo o que há para aprender sobre o círculo e uma elipse .