A parábola
Uma parábola é o local geométrico de pontos nos eixos de coordenadas que têm a propriedade que são equidistantes de um ponto fixo (chamado de foco) e uma linha (chamada diretric).
Eu sei o que parece um pouco técnico demais, mas vamos passar por isso, e no final você verá que não é tão difícil.
Então, ajudaria se eu dissesse isso
Uma função \(f(x) = x^2\) representa uma paralbola?
Certifique-se de ajudar.E você pode estar pensando "Por que você não me contou desde o início que a parábola é essa função?".
Porque não há uma parábola, há um número infinito deles.E uma parábola nem precisa ser representada por uma função.Sim, algumas relações são parabolas, como veremos.
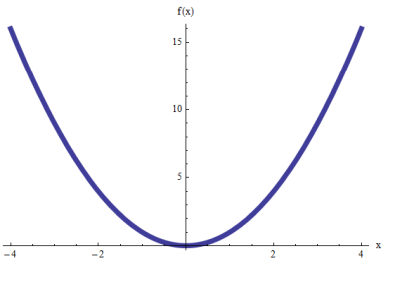
Uma coisa é importante para ser mencionada: usando funções e relações, há as parábolas que "abrem" ao longo do eixo \(y\) e existem as parábolas que "abrem" ao longo do eixo \(x\).
No final, por simetria, é fácil perceber que essas parábolas que "abrem" ao longo do eixo Y têm a mesma estrutura que aqueles que "abrem" ao longo do eixo X, por isso é suficiente para aprender alidar com um tipo.
A equação geral da parábola
Existem derivações simples para obter a equação de uma parábola com base na localização de uma diretra e no foco, mas vamos pular a derivação nesta introdução.
Verifique o gráfico abaixo.Precisamos identificar alguns elementos cruciais da parábola: temos o vértice, o foco e a directa.
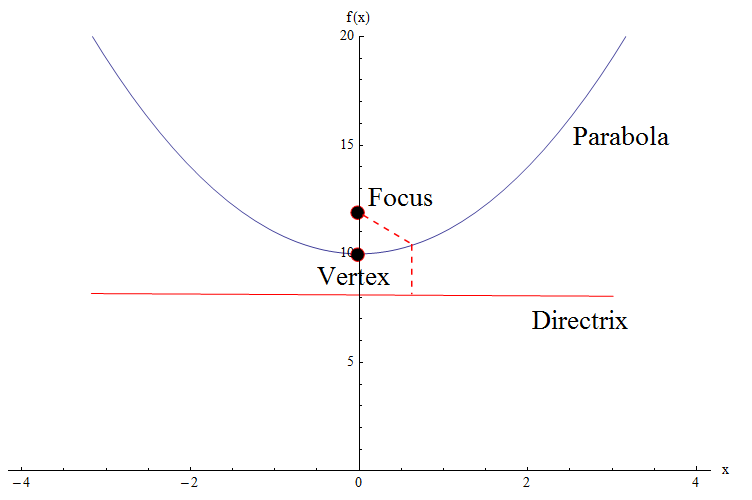
Nós não vamos em muito detalhes, mas diremos a equação de uma parábola geral com vértice na origem, com foco \((0, a)\) e diretrix igual a \(y = -a\) é
Esta parábola é o tipo de parábola que se abre ao longo do eixo Y.
Agora o que acontece quando, em vez de ter o vértice na origem, queremos ter o vértice em um determinado ponto \((k,h)\)?
Bem, essa é a magia de trabalhar com um sistema de coordenadas, e tudo o que precisamos fazer uma tradução pelo ponto ponto \((k,h)\)?Mas como você faz uma tradução por \((k,h)\)?
Simples!Onde quer que você tenha \(x\), você substitui por \(x-k\) e onde quer que tenha \(y\), substitui-lo por \(x-h\).
Assim, fazendo uma tradução, a equação de uma parábola geral com vértice no ponto \((k,h)\), com foco \((k, h+a)\) e diretrix igual a \(y = h-a\) é
\[\large y-h = 4a(x-k)^2\]que pode ser escrito como
\[\large \boxed{ y = 4a(x-k)^2 + h }\]O que acontece com os parábolos que se abrem ao longo do eixo X?
Por simetria, esta simplesmente obtida substituindo os papéis de \(x\) e \(y\) na equação da parábola já temos.Na praticidade, isso significa que, onde quer que \(x\) apareça na equação da parábola, nós a mudamos \(y\) e vice-versa para \(y\).
Portanto, a equação de uma parábola geral com vértice no ponto \((h,k)\), com foco \((h+a, k)\) e direto igual a \(x = h-a\) é:
\[\large \boxed{ x = 4a(y-k)^2 + h }\]Observe a diferença:
Quando uma parábola tem uma diretora da forma \(y = -a\), então a parábola se abre ao longo do eixo Y (para cima ou para baixo, dependendo se o foco está acima ou abaixo da directa).
Quando uma parábola tem uma diretora do formulário \(x = -a\), então a parábola abre ao longo do eixo X (esquerda ou direita, dependendo se o foco é à esquerda ou à direita da Diretriz).
EXEMPLO 1
Encontre a equação da parábola que possui um diretrix _ xyz _ a _ e um foco _ xyz_b _.Também encontre o vértice.
RESPONDER:
O vértice é o na parábola, por isso é equidistante da Diretrix \(y = -4\) e o foco \((0, 4)\), então o vértice é \(0, 0)\).Por outro lado, para uma parábola com vértice na origem, a equação da Diretrix é \(y = -a\), então neste caso \(a = 4\).Consequentemente, a equação da parábola é
\[ \large y = 4ax^2 = 4(4)x^2 = 16x^2 \]Graficamente:
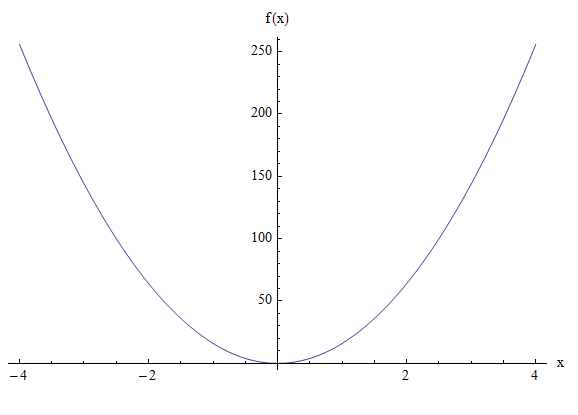
Exemplo 2.
Encontre o vértice, foco e direto da parábola \(y = 8x^2 - 16x + 9\).
RESPONDER:
Primeiro de tudo, precisamos completar o quadrado:
\[\large y = 8x^2 - 16x + 9 = 8(x^2 - 2x) + 9 \] \[\large = 8(x^2 - 2x + 1 - 1) + 9 \] \[\large = 8(x^2 - 2x + 1) + 9 - 8 \] \[\large = 8(x-1)^2 + 1 \]Equando isso com a equação geral, descobrimos que o vértice está no ponto \((1, 1)\), e também temos que \(4a = 8\), então \(a = 2\), portanto, a directrix é \(y = h - a = 1 - 2 = -1\) e o foco é \((k, h + a) = (1, 1+2) = (1, 3)\).
Graficamente:
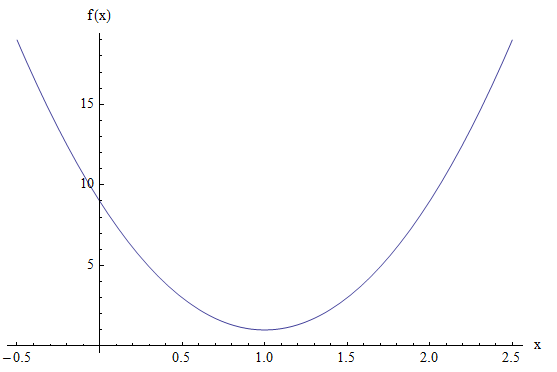
A parábola e seções cônicas gerais
Por mais estranho que seja, a parábola está firmemente relacionada ao cone.Como você diria?Um matemático grego chamado Apollonius é crédito com a versão moderna, usando sistemas de coordenadas, das seções cônicas.
Apolônio e outros matemáticos descobriram que quando você cortou um cone com um avião, dependendo do ângulo relativo do cone e do avião, o cone é cortado de uma forma que a seção tenha formas diferentes.
As diferentes formas das seções, dependendo do ângulo relativo do corte são o que conhecemos como parábola, círculo, elipse e hiperbole, como mostram na figura abaixo:
Mais sobre a parábola
Uma parábola geral que se abre ao longo do eixo Y, com vértice na origem \((0, 0)\) tem a seguinte representação funcional \(y = 4ax^2\).
Então, pela simetria, uma parábola geral que abre ao longo do eixo X, com vértice na origem \((0, 0)\) tem a seguinte representação funcional \(x = 4ay^2\).
Em seguida, um vértice geral pode ser obtido aplicando uma tradução para um determinado ponto \((k, h)\).
Formulários
A parábola tem inúmeras aplicações em física, por causa da forma como a força de gravidade e as leis de Newton operam, a trajetória da maioria dos corpos que são lançados seguirão uma trajetória parabólica.
Além disso, algebricamente falando, parábolas aparecem na Álgebra o tempo todo, porque todas as funções quadráticas têm um gráfico parabólico, e as funções quadráticas parecem muito na álgebra.
Além disso, Parabolas aparecem em cálculo ao encontrar minimas e maxima.Acontece que muitas maximizações e problemas de minimização têm uma função quadrática para maximizar e geometricamente, o máximo ou mínimo (dependendo se a parábola abrir ou para baixo) é alcançada no vértice.
Outras seções cônicas que você pode estar interessado em aprender são os elipse. , a hipérbole. e a círculo. .