Uma Elipse é o lugar geométrico dos pontos nos eixos coordenados que possuem a propriedade de que a soma das distâncias de um determinado ponto da elipse a dois pontos fixos (os focos) é igual a uma constante, que denominamos \(2a\).

O conceito de "lugar geométrico" é muito atraente do ponto de vista conceitual, mas pode não lhe dar uma visão clara do que você está tentando representar.

Experimente e faça o exercício de olhar para a equação abaixo e veja se você consegue descobrir como ela se parece graficamente;

Você poderia descobrir como funciona o gráfico apenas olhando para a equação acima. Eu pensei assim. Deixe-me apresentar a elipse para você:

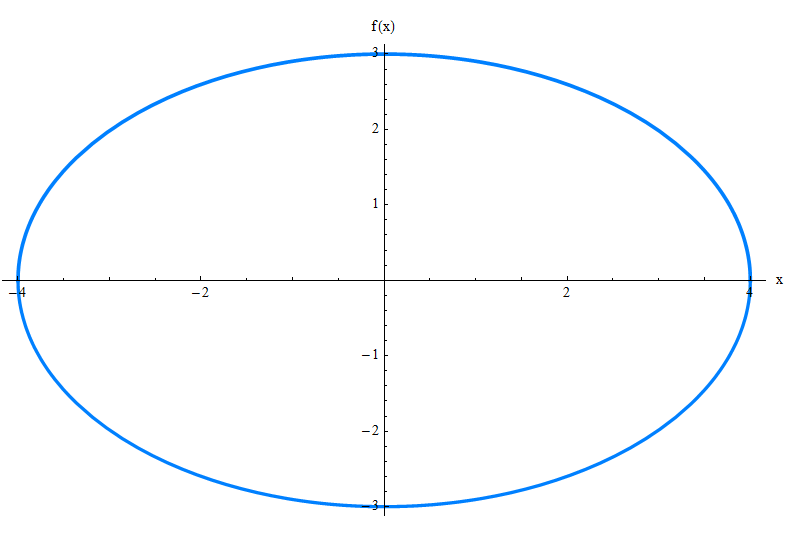
A Equação Geral da Elipse

Sem muita discussão teórica, afirmaremos que a equação geral da elipse com centro na origem e com foco no eixo x, para \(a \ge b\) é

Para a elipse descrita acima, ela possui focos nos pontos \((-c, 0)\) e \((c, 0)\), onde \(c = \sqrt{a^2 - b^2}\).

Agora, o que acontece com a equação da hipérbole acima quando \(b > a\)?

Nesse caso, os focos estão no eixo e são \((0, -c)\) e \((0, c)\), onde \(c = \sqrt{b^2 - a^2}\).

Agora, se quiser deslocar o centro para um ponto \((k,h)\)?

Nesse caso, tudo que você precisa fazer é substituir \(x\) por \(x-k\) e substituir \(y\) por \(x-h\).

Portanto, ao fazer uma tradução, obtemos que a equação de uma elipse geral é

Uma elipse acima tem um centro em \((k,h)\) e focos em \((k-c, h)\) e \((k+c, h)\) onde \(c = \sqrt{a^2 - b^2}\) para \(a \ge b\), e \((k, h-c)\) e \((k, h+c)\) onde \(c = \sqrt{b^2 - a^2}\) para \(b>a\).

EXEMPLO 1

Encontre os focos da elipse:

RESPONDA:

Em primeiro lugar, com base na estrutura da equação acima, uma elipse é centrada na origem \((0, 0)\). Observe que o semieixo maior é 4, que está associado a \(9y\), então os focos estão no eixo y.

Da equação obtivemos que \(a^2 = 9\) e \(b^2 = 16\). Encontramos que \(c = \sqrt{b^2 - a^2} = \sqrt{16 - 9} = \sqrt 7\). Portanto, os focos estão em \((0, -\sqrt{7})\) e \((0, \sqrt{7})\).

EXEMPLO 2

Encontre a equação da elipse centrada em \((0, 2)\) com um foco em \((6, 2)\) e um semi-eixo menor com tamanho 3.

RESPONDA:

Com base nas informações fornecidas, \(c = 6 - 0 = 6\). Uma vez que os focos estão em um paralelo ao eixo x, obtemos que \(b = 3\) e então \(a = \sqrt{6^2 - 3^2} = \sqrt{27}\)

Portanto, uma equação da elipse é:

A Elipse e as Seções Cônicas Gerais

Da mesma forma que no caso da parábola, da hipérbole e do círculo, a elipse está intimamente relacionada ao cone. Um matemático grego antigo chamado Apolônio conhecido essa conexão, com o que é chamado duas cônicas .

Uma seção cônica corresponde às formas que são formadas quando você faz um corte através de um cone com um plano e, exigido do ângulo relativo do cone e do plano, a forma da seção transversal muda.

Na verdade, dependendo do ângulo em que o cone e o plano se enfrentam, uma forma da seção transversal pode ser uma parábola, círculo, elipse ou hipérbole. Isso é ilustrado no gráfico abaixo: