Statistiche non parametriche o cosa fare quando i presupposti per un test parametrico falliscono

La media, la mediana e il modo sono le misure più comuni di tendenza centrale, utilizzate per descrivere il centro di una distribuzione. Dei tre, la media è quella più comunemente utilizzata, ma anche la mediana e il modo sono ampiamente utilizzati.

Dobbiamo distinguere tra i file campione media, mediana e modo e loro popolazione controparti.

In genere, lo siamo fornito con un campione e dobbiamo calcolare la media campionaria, la mediana campionaria e la modalità campionaria. Queste statistiche sono stimatori dei parametri di popolazione corrispondenti.

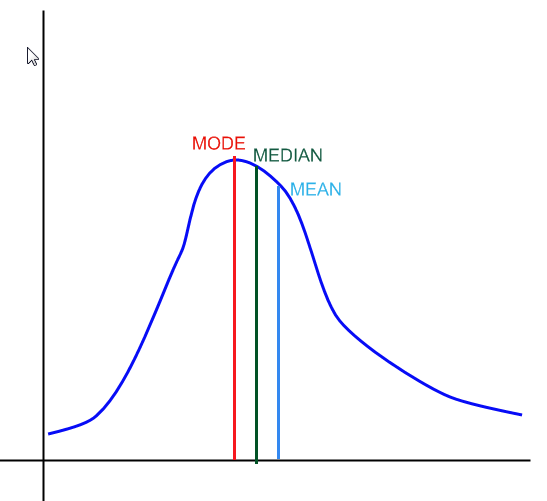
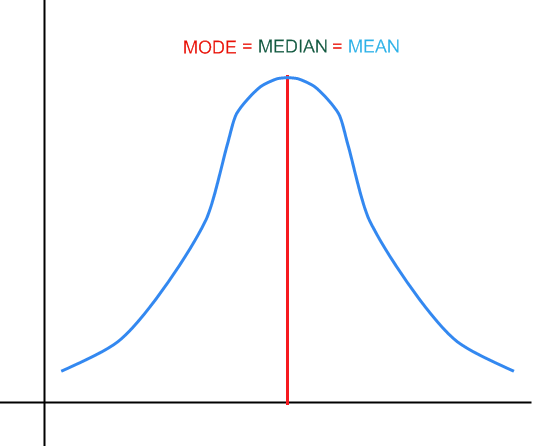
Nel grafico sopra hai un esempio di come la mediana, il modo e la media apparirebbero in una distribuzione.

La modalità corrisponde al valore più ripetuto in un campione. In una distribuzione, corrisponde al punto più alto nella funzione di densità, come mostrato nel grafico sopra.

La mediana, approssimativamente, definisce il punto in cui il 50% della distribuzione si trova a sinistra di essa ea destra di essa.

La media corrisponde alla media ponderata dei valori che la variabile assume e delle probabilità associate ($\sum x \cdot p(x)$). Per una distribuzione, tale somma ponderata è una somma o un integrale. Per un campione, calcoliamo semplicemente la media dei valori nel campione.

Come calcolare la media, la mediana e la modalità per un dato campione

Ora, supponiamo che ci venga fornito un campione $X_1, X_2, ..., X_n$ e di voler calcolare il modo, la mediana e la media. Come facciamo a tal proposito?

• Per la modalità: Semplice. Troviamo solo il numero più ripetuto. Es: se abbiamo un campione 1, 2, 2, 2, 3, 1, 4, la modalità è 2, perché 2 è il valore più ripetuto (viene ripetuto 3 volte)

• Per la mediana: Questo calcolo è leggermente più complicato. Prendi il tuo campione $X_1, X_2, ..., X_n$ e il primo passo è riorganizzarlo in ordine crescente. Quindi, supponi che $\hat X_1, \hat X_2, ..., \hat X_n$ sia il campione dopo averlo riordinato dai valori più bassi a quelli più alti.

Adesso, calcoleremo la posizione della mediana nel campione in ordine crescente. Per la dimensione del campione $n$, calcoliamo $P = 0.5 (n+1)$.

Se questo valore è un numero intero, allora troviamo che la mediana è il valore in P ^th posizione nel campione in ordine crescente.

Se questo valore NON è intero, troviamo $P_L$ e $P_U$ che sono i numeri interi più vicini a sinistra ea destra di $P$. (Es: Se $P = 10.2$, allora $P_L = 10$ e $P_U = 11$).

Quindi, la mediana è la media dei valori che si trovano nelle posizioni $P_L$ ^th e $P_U$ ^th nel campione in ordine crescente. Non preoccuparti, lo faremo con un esempio.

• Per la media: Anche semplice. La media campionaria viene calcolata utilizzando la formula

\[\displaystyle \frac{1}{n}\sum_{i=1}^n X_i\]

ESEMPIO 1

Trova la media, la mediana e la modalità per il seguente campione:

28, 36, 43, 30, 15, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 12 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51

RISPOSTA:

La tabella seguente mostra i calcoli richiesti necessari per calcolare la media

	Dati
	28
	36
	43
	30
	15
	19
	46
	36
	34
	38
	42
	29
	37
	35
	39
	39
	30
	39
	36
	38
	30
	41
	42
	46
	40
	33
	30
	40
	43
	12
	42
	39
	30
	35
	38
	41
	30
	37
	40
	30
	30
	35
	39
	37
	42
	42
	37
	38
	32
	51

Somma =	1791
Media =	35.82

La media campionaria è quindi

\[\bar{X}=\frac{1}{n}\sum{{{X}_{i}}}=\frac{1791}{50}=35.82\]

Ora per la mediana la seguente tabella mostra i dati in ordine crescente:

Dati (in ordine crescente)
12
15
19
28
29
30
30
30
30
30
30
30
30
32
33
34
35
35
35
36
36
36
37
37
37
37
38
38
38
38
39
39
39
39
39
40
40
40
41
41
42
42
42
42
42
43
43
46
46
51

In questo caso, la posizione della mediana è P = 0,5 * (50 + 1) = 25,5, quindi ${{P}_{L}}=25$ e ${{P}_{U}}=26$. Il valore nella posizione 25 ^th nei dati in ordine crescente è 37, e anche il valore nella posizione 26 è 37. La mediana è quindi

\[Median=\frac{{37}+{37}}{2}=37\]

La modalità, che è il valore più ripetuto, è 30.

Cosa è più grande, media, mediana o modalità?

Questa è una domanda che compare spesso. In termini generali, non esiste una risposta per tutte le distribuzioni. Questo è, la risposta dipende dalla distribuzione.

Per una distribuzione simmetrica abbiamo :

\[\Large \text{Mode} = \text{Median} = \text{Mean} \]

Graficamente:

Media, Mediana e Modo per una distribuzione simmetrica

Per una distribuzione asimmetrica abbiamo :

\[\Large \text{Mode} \le \text{Median} \le \text{Mean} \]

Graficamente:

Per una distribuzione asimmetrica abbiamo :

\[\Large \text{Mean} \le \text{Median} \le \text{Mode} \]

Graficamente:

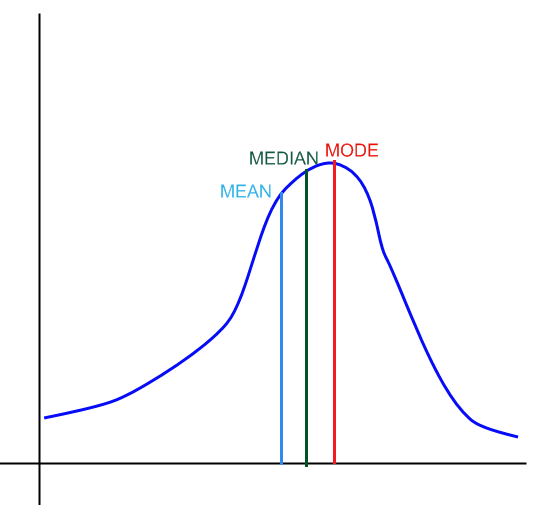
Mediana, media e modo per una distribuzione asimmetrica a sinistra

Ulteriori informazioni su media, mediana e modalità

La mediana, la media e la modalità sono ampiamente diffusi utilizzati ovunque nelle statistiche. Rappresentano misure di centro, che tentano di dare un valore rappresentativo del campione.

A seconda del livello di misurazione, utilizzeremo una misura diversa del centro.

• Per i dati nominali, usiamo la modalità.

• Per i dati ordinali e non quantitativi utilizziamo la modalità oltre alla misura del centro.

• Per i dati ordinali e quantitativi usiamo la mediana o la media come misura del centro.

• Per i dati di intervallo e rapporto, usiamo la media (o la mediana se la distribuzione è troppo asimmetrica) come misura del centro.

Applicazioni

La media, la mediana e il modo sono le misure del centro più utilizzate. La media e la mediana vengono utilizzate per i dati quantitativi e la modalità viene utilizzata per i dati categoriali.

Per i dati quantitativi, si userebbe tipicamente la media. Con un avvertimento: la media è molto sensibile ai valori anomali. Ciò significa che un valore anomalo (valore legittimo o errore di battitura) potrebbe fare una differenza drastica sul valore della media.

In questi casi, quando sono valori anomali o la distribuzione è abbastanza asimmetrica, è preferibile utilizzare la mediana come misura più accurata del centro, perché la media viene distorta dall'asimmetria o dai valori anomali.

Un esempio di ciò è quando vengono raccolti i campioni per valutare il reddito degli intervistati. Se prendiamo un campione di 100 persone e troviamo che 99 di loro guadagnano $ 10.000 all'anno e 1 persona guadagna $ 100 milioni all'anno, il reddito medio di quel campione sarebbe (10.000 * 99 + 1 * 100.000.000) / 100 = $ 1.009.900,00. Quindi, in media, tutti guadagnano $ 1.009.900,00, quindi avresti l'idea che questo campione debba provenire da un'area molto ricca, ma non è così: è solo un valore anomalo che distorce prodotto la media. In effetti, in questo caso, la mediana è $ 10.000, che è un valore del centro molto più rappresentativo per questo campione.

Calcolatrici correlate

Se hai bisogno di vedere soluzioni passo passo per il calcolo della media e altre misure di tendenza centrale, controlla calcolatrice statistica descrittiva . Puoi anche trovare utile il nostro Calcolatrice riassuntiva a 5 numeri .