Box e Whisker Plot
Il Box and Whisker Plot, o anche noto come Box-plot, è un tipo di rappresentazione grafica di un campione, che fornisce caratteristiche chiave facili da vedere della distribuzione di un campione.
Un grafico a scatola e baffi fornisce la mediana, nonché il primo e il terzo quartile nella sua "scatola", e il minimo e il massimo nel "baffo".
Quando il minimo o il massimo sono troppo estremi, "rifiliamo" il baffo e annotiamo l'esistenza di un valore anomalo.
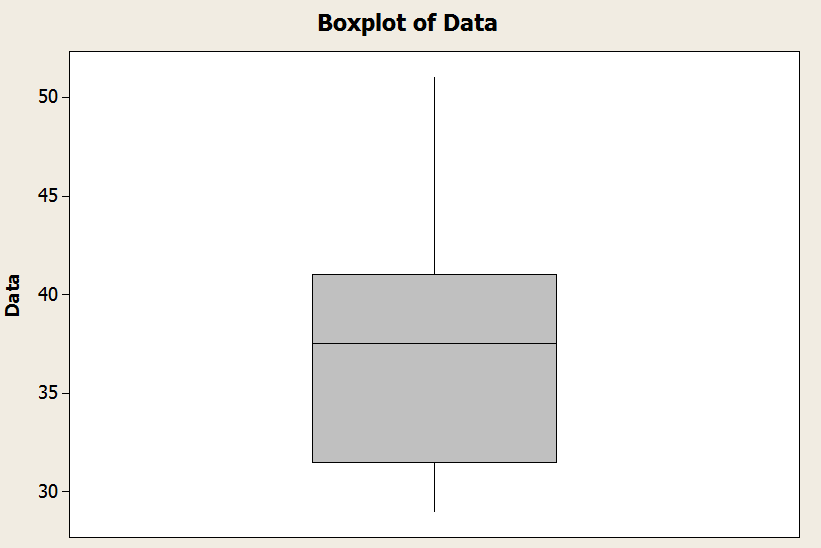
Nel grafico sopra hai un esempio di come appare un boxplot: hai la "scatola" e i baffi.
La riga inferiore del riquadro è definita dal primo quartile (\(Q_1\)).
La linea mediana della casella è definita dalla mediana (\(Q_2\)).
La riga superiore del riquadro è definita dal terzo quartile (\(Q_3\)).
Ora, per i baffi c'è una regola da seguire: il baffo inferiore è definito dal minimo del campione e il baffo superiore è definito dal massimo del campione. Viene fornito che la dimensione del baffo è inferiore a \(1.5 \times IQR\), dove \(IQR\) è l'intervallo interquartile, ed è definito da \(IQR = Q_3 - Q_1\).
Vedi il grafico di esempio sotto.
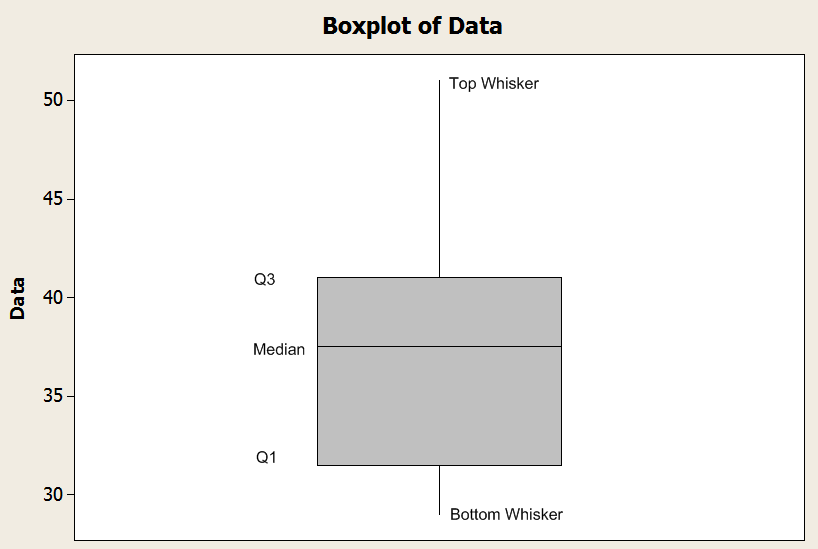
Quindi, se il minimo del campione è maggiore di \(Q_1 - 1.5 \times IQR\), il baffo inferiore è definito dal minimo. In caso contrario, è definito da \(Q_1 - 1.5 \times IQR\).
Allo stesso modo, se il massimo del campione è inferiore a \(Q_3 + 1.5 \times IQR\), il baffo superiore è definito dal massimo. In caso contrario, è definito da \(Q_3 + 1.5 \times IQR\).
ESEMPIO 1
Costruisci un box-plot per il seguente esempio:
28, 36, 43, 30, 46, 19, 46, 36, 34, 38, 42, 29, 37, 35, 39, 39, 30, 39, 36, 38, 30, 41, 42, 46, 40, 33, 30, 40, 43, 30, 42, 39, 30, 35, 38, 41, 30, 37, 40, 30, 30, 35, 39, 37, 42, 42, 37, 38, 32, 51
RISPOSTA:
Otteniamo che il massimo e il minimo siano
\[\min = 19\] \[\max = 51\]La tabella seguente mostra i dati in ordine crescente:
|
Dati (in ordine crescente) |
|
19 |
|
28 |
|
29 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
32 |
|
33 |
|
34 |
|
35 |
|
35 |
|
35 |
|
36 |
|
36 |
|
36 |
|
37 |
|
37 |
|
37 |
|
37 |
|
38 |
|
38 |
|
38 |
|
38 |
|
39 |
|
39 |
|
39 |
|
39 |
|
39 |
|
40 |
|
40 |
|
40 |
|
41 |
|
41 |
|
42 |
|
42 |
|
42 |
|
42 |
|
42 |
|
43 |
|
43 |
|
46 |
|
46 |
|
46 |
|
51 |
La mediana è quindi
\[Median=\frac{{37}+{38}}{2}=37.5\]La posizione del 25 ° percentile è
\[{{L}_{25}}=\frac{P}{100}\times \left( n+1 \right)=\frac{25}{100}\times \left( 50+1 \right) = {12.75}\]Quindi, lo otteniamo
\[{{Q}_{1}}={30} +{0.75}\times \left( {32}-{30} \right) = {31.5}\]La posizione del 75 ° percentile è
\[{{L}_{75}}=\frac{P}{100}\times \left( n+1 \right)=\frac{75}{100}\times \left( 50+1 \right) = {38.25}\]Quindi, lo otteniamo
\[{{Q}_{3}}={41}+{0.25}\times \left( {41}-{41} \right) = {41}\]Quindi, il riepilogo a 5 numeri è
\[\min = 19, Q_1 = 31.5, Q_2 = 37.5, Q_3 = 41, \max = 51\]L'intervallo interquartile in questo caso è \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). Quindi,
\(Q_1 - 1.5 \times IQR = 31.5 - 1.5 \times 9.5 = 17.25\)
\(Q_3 + 1.5 \times IQR = 41 + 1.5 \times 9.5 = 55.25\)
Osserva che il minimo è 19 ed è maggiore di \(Q_1 - 1.5 \times IQR = 17.25\). E il massimo è 51 ed è inferiore a \(Q_3 + 1.5 \times IQR = 55.25\).
Concludiamo che il baffo inferiore è il minimo e il baffo superiore è il massimo in questo caso. Graficamente
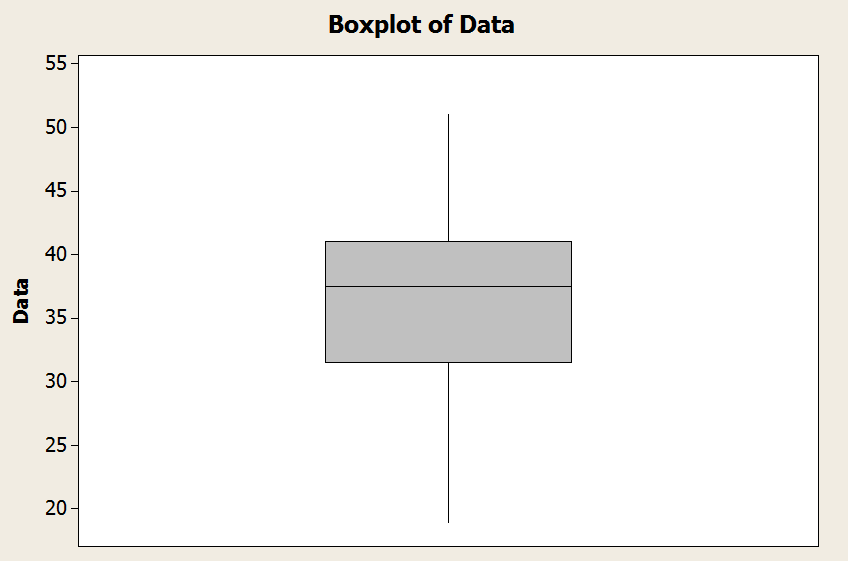
ESEMPIO 2
Trova il box plot per lo stesso campione dell'esempio precedente, ma quando sostituisci "51" con "81".
RISPOSTA:
Otteniamo che il massimo e il minimo siano
\[\min = 19\] \[\max = 81\]La tabella seguente mostra i dati in ordine crescente:
|
Dati (in ordine crescente) |
|
19 |
|
28 |
|
29 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
30 |
|
32 |
|
33 |
|
34 |
|
35 |
|
35 |
|
35 |
|
36 |
|
36 |
|
36 |
|
37 |
|
37 |
|
37 |
|
37 |
|
38 |
|
38 |
|
38 |
|
38 |
|
39 |
|
39 |
|
39 |
|
39 |
|
39 |
|
40 |
|
40 |
|
40 |
|
41 |
|
41 |
|
42 |
|
42 |
|
42 |
|
42 |
|
42 |
|
43 |
|
43 |
|
46 |
|
46 |
|
46 |
|
81 |
La mediana è quindi
\[Median=\frac{{37}+{38}}{2}=37.5\]La posizione del 25 ° percentile è
\[{{L}_{25}}=\frac{P}{100}\times \left( n+1 \right)=\frac{25}{100}\times \left( 50+1 \right) = {12.75}\]Quindi, lo otteniamo
\[{{Q}_{1}}={30} +{0.75}\times \left( {32}-{30} \right) = {31.5}\]La posizione del 75 ° percentile è
\[{{L}_{75}}=\frac{P}{100}\times \left( n+1 \right)=\frac{75}{100}\times \left( 50+1 \right) = {38.25}\]Quindi, lo otteniamo
\[{{Q}_{3}}={41}+{0.25}\times \left( {41}-{41} \right) = {41}\]Quindi, il riepilogo a 5 numeri è
\[\min = 19, Q_1 = 31.5, Q_2 = 37.5, Q_3 = 41, \max = 81\]L'intervallo interquartile in questo caso è \(IQR = Q_3 - Q_1 = 41 - 31.5 = 9.5\). Quindi,
\(Q_1 - 1.5 \times IQR = 31.5 - 1.5 \times 9.5 = 17.25\)
\(Q_3 + 1.5 \times IQR = 41 + 1.5 \times 9.5 = 55.25\)
Osserva che il minimo è 19 ed è maggiore di \(Q_1 - 1.5 \times IQR = 17.25\). Ma ora il massimo è 81, che supera \(Q_3 + 1.5 \times IQR = 55.25\). Pertanto, il valore "81" è un valore anomalo.
Concludiamo che il baffo inferiore è il minimo e il baffo superiore è definito da \(Q_3 + 1.5 \times IQR = 55.25\). Graficamente
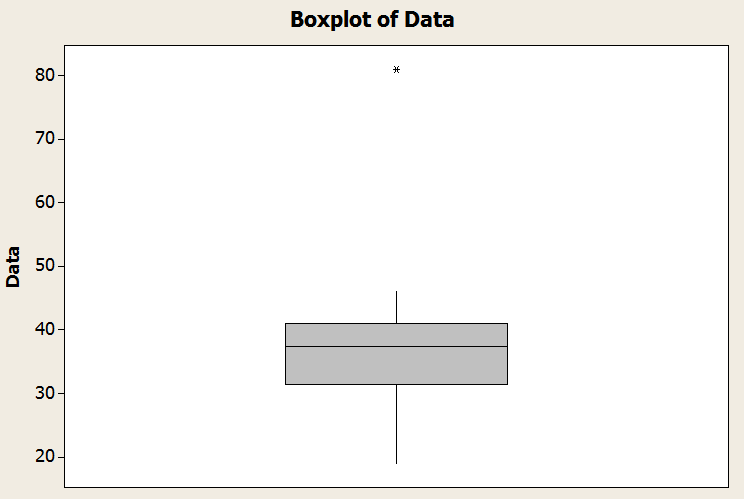
Ulteriori informazioni sul Boxplot
La domanda principale delle persone è cosa ti dicono i boxplots. Cosa rappresentano. E la risposta è semplice: ti danno una rappresentazione riassunta della distribuzione di un campione fornendo un grafico schematico che mostra la posizione relativa del Riepilogo a 5 numeri .
In questo modo, puoi eseguire la scansione valori anomali , puoi valutare il grado di asimmetria della distribuzione e puoi scansionare rapidamente le regioni che hanno il 25%, 50% e 75% della distribuzione totale.
Differenza tra Box-plot e Istogramma
Uno degli aspetti del box plot è che fornisce informazioni leggermente diverse dalle informazioni fornite da un istogramma.
Infatti, l'istogramma mostra la forma grezza della distribuzione, basata sulle classi utilizzate per classificare i possibili valori della variabile casuale. D'altra parte, il boxplot fornisce informazioni riepilogative sui quartili e il riepilogo a 5 numeri, che ti dice molto sulla posizione relativa del primo e del terzo quartile rispetto alla mediana.
Quindi, in altre parole, il boxplot, a differenza dell'istogramma, presenta un grafico che rappresenta un file riepilogo della distribuzione , piuttosto che una rappresentazione grezza. Gli unici valori grezzi che andrebbero in un grafico a scatole sarebbero i valori anomali (se ce ne sono).
Applicazioni
L'applicazione più classica per il box plot è per rilevare i valori anomali. Per definizione, il box plot limita la dimensione dei baffi a 1,5 volte l'intervallo interquartile \((IQR)\) dalle estremità del riquadro (che sono definiti da \(Q_1\) e \(Q_3\).
Quindi, quindi, tutti i punti che vanno oltre la dimensione massima dei baffi verranno annotati nel box-plot e saranno considerati valori anomali.
Metti in pratica i concetti che hai imparato in questo tutorial usando questo creatore di box-plot . Un altro grafico che permetterà di vedere in un colpo d'occhio le proprietà distributive della distribuzione di un campione è questo creatore di istogrammi , o questo creatore di grafici a stelo e foglia .