Disuguaglianze di valore assoluto
Le disuguaglianze di valore assoluto sono disuguaglianze in cui sono presenti una o più valore assoluto . Ricordiamo che una disuguaglianza è quasi come un'equazione, ma invece del segno "=" abbiamo "≤" o "≥".
Questa differenza fa sì che l'insieme di soluzioni sia tipicamente una regione, come per la maggior parte delle disuguaglianze. E il fatto che ci siano valori assoluti coinvolti indica un certo trattamento speciale per la loro risoluzione.
In questo tutorial ci concentreremo sulle abilità specifiche richieste per la risoluzione di questo tipo di disuguaglianza che contiene uno o più valori assoluti. Inoltre, assumeremo che una o due variabili, \(x\) e / o \(y\) siano coinvolte nella disuguaglianza.
Che cos'è una disuguaglianza di valore assoluto?
Ai fini di questa analisi, considereremo una disuguaglianza di valore assoluto come una disuguaglianza che coinvolge una o due variabili, con almeno un valore assoluto.
Ad esempio, di seguito abbiamo una disuguaglianza di valore assoluto con due variabili \(x\) e \(y\):
\[|3x+2y-1| \ge 1\]Oppure, potremmo avere la seguente disuguaglianza di valore assoluto con una sola variabile:
\[|3x-1| \le 2\]Per i nostri scopi, e ai fini delle tecniche utilizzate per la loro risoluzione, ci occuperemo di entrambi i tipi di disuguaglianze (una e due variabili)
Come risolvere le disuguaglianze di valore assoluto?
Quando si risolvono equazioni o disequazioni, non c'è davvero un proiettile d'argento che risolva tutto. Ogni problema è diverso e può avere le sue peculiarità.
Il meglio che possiamo fare è fornire una serie di passaggi che ti aiuteranno nel processo di risoluzione di una disuguaglianza.
Passo 1:
Per ogni assoluto determinare le regioni in cui l'argomento del valore assoluto è negativo e dove non è negativo.
Passo 2:
Se c'è un solo valore assoluto nella disuguaglianza, risolverlo in entrambe le aree (dove l'argomento del valore assoluto è negativo e dove non è negativo).
Passaggio 3:
Se c'è più di un valore assoluto nella disuguaglianza, è necessario intersecare tutte le regioni per ottenere un insieme di partizioni più piccole. In ogni partizione, è necessario conoscere ESATTAMENTE il segno di ogni argomento. Quindi, risolvi la disuguaglianza in tutte le aree.
Passaggio 4:
Una volta ottenuta la soluzione della parte che si trova in ciascuna delle aree, la soluzione finale è semplicemente l'unione di queste soluzioni della parte.
In parole semplici: devi scoprire le regioni in cui conosci esattamente il segno dell'argomento dei valori assoluti (così puoi sbarazzartene).
Un paio di esempi dovrebbero chiarire questi passaggi.
ESEMPIO 1
Risolvi la seguente disuguaglianza
\[| 2x + 4y - 1 | \ge 2\]RISPOSTA:
Per risolvere la disuguaglianza, dobbiamo utilizzare i passaggi specificati sopra.
Passo 1: C'è solo un valore assoluto, quindi dobbiamo determinare se l'argomento è negativo e non negativo. Pertanto, dobbiamo prima risolvere:
\[2x + 4y - 1 \ge 0\]Esistono diverse strategie per risolvere quanto sopra, ma la più semplice è risolvere prima l'equazione
\[2x + 4y - 1 = 0\]il che significa che \(4y = -2x + 1\) o uguale a \(y = -\frac{1}{2}x + \frac{1}{4}\), che corrisponde a una linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = \frac{1}{4}\).
Ora, per occuparci di \(2x + 4y - 1 \ge 0\) testiamo se il punto \((0,0)\) soddisfa o meno la disuguaglianza:
\[2(0) + 4(0) - 1 = -1 < 0\]Quindi, \((0,0)\) soddisfa o meno la disuguaglianza. La conclusione è che la linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = \frac{1}{4}\) divide il piano in due regioni:
Per i punti sotto la linea (chiamiamo questa regione 1, \(R_1\)), otteniamo che \(2x + 4y - 1 < 0\)
Per i punti sopra la linea, inclusa la linea stessa (chiamiamo questa regione 2, \(R_2\)) otteniamo che \(2x + 4y - 1 \ge 0\)
Perché questo è importante? Perché ci prendiamo tutto questo disturbo? Perché su \(R_1\), lo otteniamo da \( 2x + 4y - 1 < 0\), poi \(| 2x + 4y - 1 | = -(2x + 4y - 1) \). Allo stesso modo, su \(R_2\), lo otteniamo da \( 2x + 4y - 1 \ge 0\), quindi \(| 2x + 4y - 1 | = 2x + 4y - 1 \).
Passo 2: Ora dobbiamo risolvere la disuguaglianza nella regione 1, \(R_1\) :
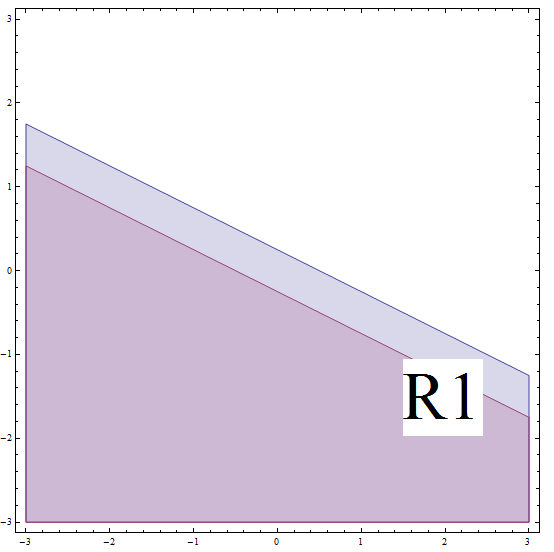
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]Ciò corrisponde a tutti i punti sotto o sulla linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = -\frac{1}{4}\). Ma non dimenticare che sei su \(R_1\) e questa linea che abbiamo trovato è SOTTO il confine di \(R_1\) (guarda il grafico sotto).
Per chiarire, dal momento che stiamo assumendo che siamo in \(R_1\), dobbiamo avere che siamo SOTTO la linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = \frac{1}{4}\). Sotto questo presupposto, abbiamo risolto la disuguaglianza originale e dobbiamo anche essere sotto la linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = -\frac{1}{4}\). Queste due condizioni devono verificarsi contemporaneamente, quindi otteniamo l'intersezione delle due regioni.
Quindi, la soluzione della parte in questo caso corrisponde a tutti i punti sotto o sulla linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = -\frac{1}{4}\).
Ora dobbiamo risolvere la disuguaglianza nella regione 2, \(R_2\) :
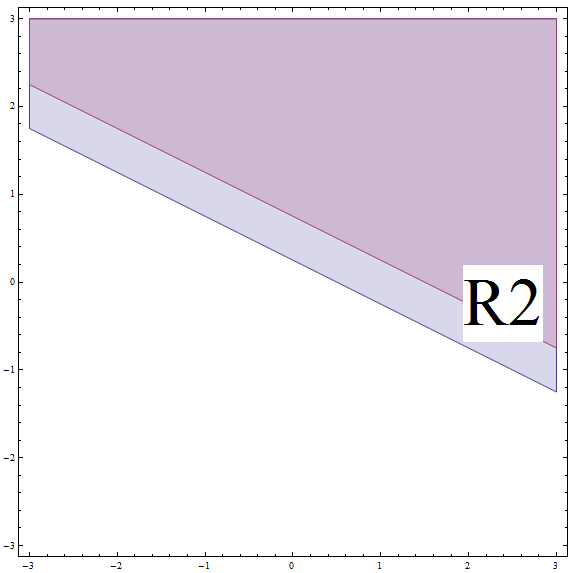
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]Ciò corrisponde a tutti i punti sopra o sulla linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = \frac{3}{4}\). Ma non dimenticare che sei su \(R_2\) e questa linea è SOPRA il limite di\(R_2\) (vedi il grafico sotto).
Trovando l'intersezione tra \(R_2\) e la regione sopra, otteniamo che la soluzione della parte in questo caso sono tutti i punti sopra o sulla linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = \frac{3}{4}\).
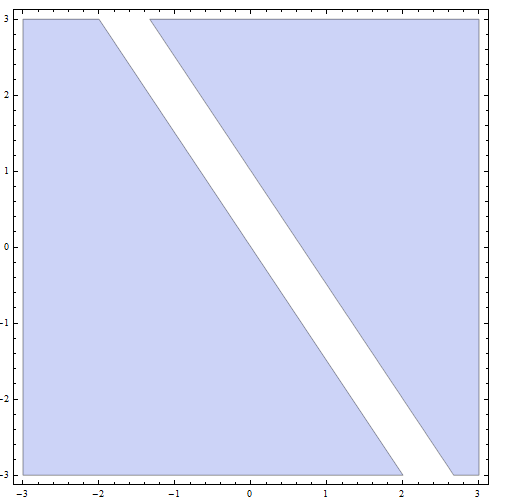
Passaggio 4: Ora, la soluzione finale è l'unione di tutte le soluzioni delle parti delle parti precedenti: la soluzione finale sono tutti i punti SOTTO o sulla linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = -\frac{1}{4}\), PIÙ tutti i punti SOPRA o sulla linea con pendenza \(m = -\frac{1}{2}\) e intercetta y \(n = \frac{3}{4}\).
Graficamente, otteniamo
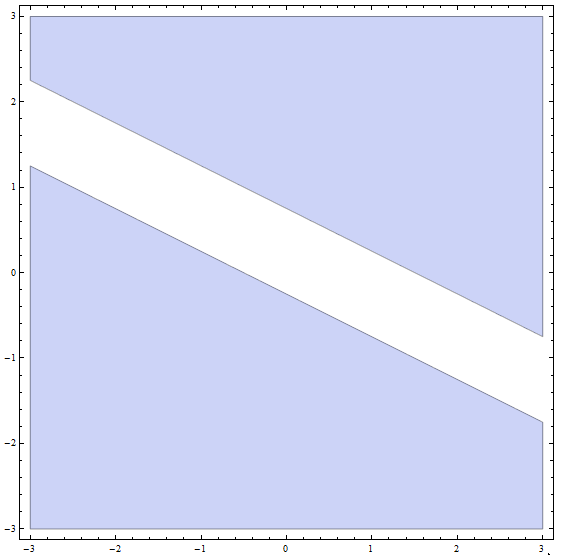
che conclude la risoluzione della disuguaglianza.
ESEMPIO 2
Risolvi la seguente doppia disuguaglianza del valore assoluto
\[| 2x - 1 | \ge |x + 3|\]RISPOSTA:
Questa è una doppia disuguaglianza del valore assoluto perché ci sono 2 valori assoluti. Ciò significa che trovare le regioni richiederà un po 'più di lavoro (relativamente parlando).
Passo 1: Per il primo valore assoluto risolviamo:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]Quindi otteniamo \(2x- 1 \ge 0\) su \([\frac{1}{2}, +\infty)\) e \(2x- 1 < 0\) su \((-\infty, \frac{1}{2})\).
Per il secondo valore assoluto risolviamo:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]Quindi otteniamo \(x+3 \ge 0\) su \([-3, +\infty)\) e \(x+3 < 0\) su \((-\infty, -3)\).
Quindi, definiamo 4 regioni:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). In questa regione otteniamo: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). In questa regione otteniamo: \(2x- 1 \ge 0\) AND \(x+3 < 0\), sebbene questa regione sia vuota.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). In questa regione otteniamo: \(2x- 1 < 0\) AND \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). In questa regione otteniamo: \(2x- 1 < 0\) AND \(x+3 < 0\).
Passo 2: Ora dobbiamo risolvere la doppia disuguaglianza del valore assoluto su ciascuna delle quattro regioni:
• Il \(R_1\):
Qui otteniamo \(2x- 1 \ge 0\) AND \(x+3 \ge 0\) quindi
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]Quindi, per ottenere la soluzione della parte, dobbiamo intersecare \(x \ge 4\) o \([4, +\infty)\) con \(R_1\).
La soluzione della parte corrispondente è quindi: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• Il \(R_2\):
Questa soluzione parziale è vuota (\(\varnothing\)).
• Il \(R_3\):
Qui otteniamo \(2x- 1 < 0\) AND \(x+3 \ge 0\) quindi
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]Quindi, per ottenere questa soluzione di parte, dobbiamo intersecare \( x \le -\frac{2}{3}\) o \( (-\infty, -\frac{2}{3}]\) con \(R_3\).
La soluzione della parte corrispondente è quindi: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• Il \(R_4\):
Qui otteniamo \(2x- 1 < 0\) AND \(x+3 < 0\) quindi
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]Quindi, per ottenere questa soluzione di parte, dobbiamo intersecare \( x \le 4 \) o \((-\infty, 4]\) con \(R_4\).
La soluzione della parte corrispondente è quindi: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
Passaggio 4:
Infine, otteniamo l'unione delle soluzioni delle parti, per ottenere che la soluzione della disuguaglianza data iniziale sia
Nessuno ha detto che sarebbe stato breve, giusto? Bene. Non è davvero difficile, devi solo essere sistematico e attenersi al piano.
Ulteriori informazioni sulle disuguaglianze con valore assoluto
Perché ci preoccupiamo anche di questo tipo di disuguaglianze? Ci preoccupiamo perché hanno applicazioni nella pratica.
Ad esempio, in geometria, le distanze nella linea reale devono essere rappresentate come un valore assoluto, perché deve essere non negativo.
Si potrebbe avere una certa situazione geometrica in cui è necessario trovare tutti i punti della retta reale che siano almeno ad una distanza di 2 dal punto 3. Tale situazione può essere descritta con la seguente disuguaglianza:
\[| x-3 |\ge 2\]Cerchiamo di capire la disuguaglianza di cui sopra. Il punto \(x\) è il punto in cui vogliamo soddisfare la disuguaglianza. La distanza da \(x\) al punto 3 è rappresentata da \(|x - 3|\).
Quindi, stiamo cercando di trovare i punti che sono almeno a una distanza di 2 dal punto 3, quindi la distanza \(|x - 3|\) deve essere almeno 2, il che spiega \(|x - 3| \ge 2.\)
Questo è solo un tipo di problemi di disuguaglianze di valore assoluto che puoi trovare nella pratica.
Riesci a trovare disuguaglianze di valore assoluto senza soluzione
Scommetti. Eccone uno \(|2x| < |x|\). È possibile che una disuguaglianza sia semplicemente irrealizzabile come nel caso di questa che ti ho appena fornito.
Che ne dici di rappresentare graficamente le disuguaglianze di valore assoluto?
Il processo di rappresentarli graficamente è essenzialmente di pari passo con il processo di risolverli: è necessario trovare le regioni in cui si sa esattamente se gli argomenti dei valori assoluti sono positivi o negativi, e quindi le disuguaglianze di valore assoluto diventano semplici disuguaglianze, che è banalmente rappresentato graficamente. Quindi, tutti i pezzi delle regioni ottenute vengono semplicemente uniti.