Metodo di integrazione sostitutivo
Il metodo di integrazione per sostituzione o il metodo di integrazione per sostituzione è una tecnica intelligente e intuitiva utilizzata per risolvere gli integrali e svolge un ruolo cruciale nel compito di risolvere gli integrali, insieme al integrazione per parti e decomposizione delle frazioni parziali metodo.
L'integrazione può essere un'operazione difficile a volte e abbiamo solo pochi strumenti a disposizione per procedere con essa.
Naturalmente, il calcolo dell'integrale indefinito per alcune funzioni elementari di base (come polinomi, potenze, funzioni trigonometriche elementari, ecc.) È molto semplice.
Ma la domanda è come procedere con il calcolo dell'integrale indefinito (o primitivo) per funzioni più complesse o per la combinazione algebrica di funzioni.
Sei pronto per il rock ?? Lo sono, quindi seguimi.
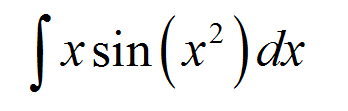
Come funziona il metodo di sostituzione?
Il metodo di integrazione per sostituzione funziona identificando un "blocco" che contiene la variabile di integrazione, in modo che la derivata di quel blocco si trovi anche all'interno dell'integrale. Questo metodo è anche comunemente chiamato metodo di sostituzione u.
Se la struttura dell'integrale lo consente, questo "blocco" diventa effettivamente una nuova variabile di integrazione, se tutto va bene, e l'integrale si semplifica seriamente.
Funziona sempre? No. O detto diversamente, puoi sempre fare una sostituzione, ma non sempre la convertirà in un integrale più semplice.
Perché anche provare questo metodo? Bene, perché funziona spesso. Ed è in genere il primo trucco che dovresti provare se devi risolvere un integrale che non è banale.
Mettiamo un paio di passaggi da seguire se è necessario applicare questo metodo:
PASSO 1:
Esamina la funzione che stai integrando e cerca un "blocco", questa è una funzione di \(x\) che appare una o più volte nella funzione che stai integrando.
PASSO 2:
Il "blocco" che stai cercando deve avere una proprietà ben precisa: la derivata del blocco deve comparire una volta e una sola volta nella funzione che si sta integrando.
FASE 3:
Se i passaggi precedenti hanno avuto successo, puoi usare il "blocco" come nuova variabile e puoi sostituire la variabile e il differenziale con la nuova variabile, e l'integrale che stai risolvendo ora diventa molto più semplice.
Nota tecnica : Di solito cerco di mantenere tutte le spiegazioni semplici e cerco di evitare tecnicismi. In questo caso dovrò dare la spiegazione tecnica del metodo di sostituzione, per non lasciare le cose troppo informali con l'idea del "blocco".
Se non ti piacciono i tecnicismi, puoi passare alla sezione successiva, dove vedrai gli esempi.
Quindi, l'idea è di integrare una data funzione \(f(x)\). Quindi dobbiamo trovare:
\[\int f(x) \, dx\]Supponiamo che la funzione \(f(x)\) non sia una funzione qualsiasi e abbia una certa struttura specifica, in particolare
\[f(x) = g(h(x))h'(x)\]e supponiamo che esista una funzione \(G(x)\) in modo che \(G'(x) = g(x)\) (quindi \(G\) è l'antiderivativa di \(g\)). Quindi, lo otteniamo
\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]Perché??? Bene, semplice: per definizione, una antiderivativa è una funzione in modo che quando la differenziate, ottenete la funzione che state integrando.
In questo caso, se differenzi \( G(h(x)) \) ottieni
\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]dalla regola della catena ..... e shazam! lo avete. Te l'avevo detto che non era così difficile.
Esempi di metodi di sostituzione
Il modo migliore per imparare a integrare è esercitarsi. Alcune persone si rallegreranno nel guardare le prove, ma la maggior parte delle persone vorrà vedere le cose in pratica.
Quindi, passiamo a motivi pratici.
ESEMPIO 1
Trova il seguente integrale indefinito:
\[\int x \sin(x^2)\,dx\]RISPOSTA:
Secondo il passaggio 1, stiamo cercando un blocco, un blocco molto specifico. Se guardi l'integrale, la variabile di integrazione è \(x\).
Ci sono molti tentativi ed errori, potenzialmente, quando si utilizza questa tecnica. Diciamo che consideriamo il seguente blocco:
\[u = x^2\]Sappiamo che questo blocco è buono perché la sua derivata è \(u' = 2x\), che appare nell'integrale.
Ma poi dici "Vedo il \(x\) ma non vedo il 2". Bene, non è necessario essere tesi. Possiamo fare un trucco. Osservalo
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]Chi sei, Mandrake the Magician ??? Scherzi a parte, quel piccolo trucco funziona. Quindi, la sostituzione del blocco è
\[u = x^2\] \[du = 2x \, dx\](la notazione di \(du = 2x \, dx\) è permissiva e tecnicamente errata, ma ha solide basi, quindi sopportatela). Quindi fare questa sostituzione trasforma l'integrale in
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]Quindi, una volta modificato nella nuova variabile \(u\), l'integrale è diventato un integrale più facile da risolvere di \(\sin(u)\). Una volta risolto, DEVI ricordarti di tornare alla variabile originale.
ESEMPIO 2
Passiamo ora a un esempio leggermente più complicato. Calcola l'integrale indefinito
\[\int e^{x+e^x} \,dx\]utilizzando il metodo di sostituzione u.
RISPOSTA:
Cos'è questo che dici ??? Beh, non è così difficile. Si noti che l'integrale indefinito può essere riscritto come:
\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]Quindi, ora che vedi la nuova forma della funzione che stai integrando, puoi inventare un "blocco" o una "sostituzione u" ??
Ricorda, non essere timido di fare tentativi ed errori. Se qualcosa non funziona, prova qualcos'altro. E se provassi \(u = e^x\)?
La derivata del blocco è \(u' = e^x\), che si trova una volta nella funzione originale. Inoltre:
\[u = e^x\] \[du = e^x \, dx\]Quindi otteniamo:
\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]Ulteriori informazioni sull'integrazione per sostituzione
Ammettiamolo: l'integrazione può essere difficile. Davvero difficile. Alcune funzioni non troppo complicate (almeno dall'aspetto) hanno dato ai matematici un momento terribilmente difficile da affrontare.
Alcune altre funzioni non troppo complicate (almeno a giudicare dall'aspetto) semplicemente non sono risolvibili con metodi elementari.
Quindi, faresti meglio a credere che l'integrazione possa essere una dura prova. Quindi devi essere preparato.
Uno degli strumenti più semplici e una tecnica molto comunemente usata è la tecnica dell'integrazione per sostituzione. Sì, viene utilizzato perché appare frequentemente durante i test o i compiti.
Ma abbiamo imbrogliato un po '. In realtà, gli integrali che hanno la struttura giusta per essere risolti con la tecnica di sostituzione sono molto specifici. Il motivo per cui vedi molti esempi di questo è perché sono funzioni molto specifiche che dovrebbero funzionare per essere integrate con quella tecnica.
Ma permettimi di essere schietto: se hai un programma software progettato per generare funzioni casuali, e ne genera uno per te, le possibilità che sarai in grado di utilizzare la tecnica di sostituzione sono scarse.
Tuttavia, è una piccola e potente tecnica di integrazione che funziona per una classe molto specifica di integrali.
Qual è la tecnica di sostituzione a U?
La sostituzione 𝘶 con integrali indefiniti è solo un altro nome per il metodo di sostituzione. Si chiama "𝘶-sostituzione" perché il blocco che viene utilizzato si chiama \(u\), quindi la nuova variabile sarà u.
Questo non è sicuramente un buon nome, perché il nome che scegli per il tuo blocco è completamente irrilevante per il processo di calcolo dell'integrale. Puoi chiamare il blocco (e la tua nuova variabile) \(z\) e non farebbe differenza.