L'eliminazione gaussiana è un processo condotto su matrici finalizzate a inserire una matrice forma a scaglione . Avere una matrice in tale forma aiuta enormemente a risolvere le equazioni di matrice molto facilmente.

Tecnicamente, il processo di conduzione dell'eliminazione gaussiana consiste nel trovare una colonna con un perno (che è il gergo di fantasia per un elemento diverso da zero) che ci permette di eliminare tutti gli elementi al di sotto del perno.

Questo processo di ricerca di perni ed eliminazione ci consente di mettere una matrice in forma di scaglione, e il modo in cui procede è tale che ruotando si aggiunge una nuova colonna al modulo di scaglione e non si 'rovina' il modulo di scaglione hanno recuperato il passaggio precedente. Bello se me lo chiedi.

Il termine "forma a scaglione" che si ottiene usando l'eliminazione gaussiana diventa chiaro guardando la matrice sopra, dove gli elementi diversi da zero della matrice hanno questa struttura a scaglione, come mostrato dalla linea rossa.

La matematica dietro il pivot e l'eliminazione gaussiana

Non entreremo troppo nel tecnico, proveremo solo a farti capire la motivazione e la meccanica di questo tipo di eliminazione.

L'idea è di ottenere una matrice $A$, di dimensione $m \times n$ (cioè, ha $m$ righe e $n$ colonne) in una forma diversa che sia più adatta alla risoluzione di equazioni.

Più specificamente, per una matrice $m\times n$ $A$ e un vettore $m\times 1$ $b$, dobbiamo trovare un vettore $n\times 1$ $x$ tale che

Potresti pensare, "è così facile, moltiplichiamo semplicemente ciascun lato per $A^{-1}$ da sinistra", quindi otteniamo:

....Non così in fretta! Funziona solo quando la matrice $A$ è invertibile. Per iniziare, la matrice $A$ deve essere una matrice quadrata e quindi il suo determinante deve essere diverso da zero. Ma non puoi moltiplicare per l'inverso per matrici non quadrate. Allora, come lo fai allora?

Devi TRASFORMARE l'equazione in una più facile da risolvere.

Nello specifico, le matrici in forma di scaglioni sono matrici che portano a equazioni facili da risolvere (ne parleremo più avanti).

Utilizzo di matrici elementari

Prima di tutto, faremo una nota cruciale. Se abbiamo una soluzione dell'equazione della matrice $Ax = b$ e $E$ è una matrice invertibile, allora $x$ è anche una soluzione di $(EA)x = Eb$ e viceversa.

In altre parole, le equazioni di matrice

e

sono equivalenti, per una matrice invertibile $E$. Cosa intendiamo con che le equazioni sono equivalenti? Intendiamo che le equazioni hanno le stesse soluzioni.

Quindi quello che faremo è iniziare con $Ax = b$ e, moltiplicando per matrici invertibili $E$, arriveremo a un'equazione di matrice equivalente che è molto più facile da risolvere .

Diciamo che siamo in grado di trovare un elenco di matrici invertibili $E_1, E_2, ..., E_n$ e moltiplichiamo (da sinistra) l'equazione della matrice originale per trasformarla in un'equazione equivalente, come:

dove $E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A$ e $E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b$.

Il nostro obiettivo è con attenzione scegliere le matrici invertibili $E_1, E_2, ..., E_n$ in modo che $\tilde A$ sia in forma di scaglione.

Perché? Perché se $\tilde A$ è in forma scaglionata, risolvere l'equazione della matrice $\tilde A x = \tilde b$ è molto più semplice e sappiamo già che $\tilde A x = \tilde b$ ha le stesse soluzioni di $A x = b$

ESEMPIO 1

Vediamo perché risolvere un'equazione di matrice è molto più semplice quando lo si ha in forma di scaglioni. Per prima cosa immagina di avere la seguente matrice e vettore:

e vuoi risolvere $Ax = b$. Come sarebbe il sistema di equazioni? Il sistema $Ax = b$ sarebbe simile

Come sembra? Beh, non così pulito. Avresti bisogno di iniziare a destreggiarti tra le equazioni. Esistono approcci più o meno sistematici per risolvere questo problema utilizzando cose come l'eliminazione e simili, ma è almeno complicato.

Ora, d'altra parte, immagina di avere la seguente matrice e vettore:

e vuoi risolvere $\tilde A x = \tilde b$. In questo caso, la matrice $\tilde A$ è in formato scaglione. Come sarebbe il sistema di equazioni? Il sistema $\tilde A x = \tilde b$ sarebbe simile

Come appare questo? Beh, non troppo malandato.

Infatti, se partiamo direttamente dalla terza equazione, abbiamo quella $x_3 = -1$ direttamente. Quindi dalla seconda equazione, $x_2 = -1 + x_3 = -1 + (-1) = -2$. E dalla prima equazione, $x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4$. Quindi senza alcun fuzz, abbiamo scoperto che:

Pertanto, in questo caso il sistema si risolve banalmente.

Per i sistemi associati a matrici in forma di scaglioni, è semplice tornare indietro dall'ultima equazione alla prima equazione, per ottenere le soluzioni.

Come scegliere le giuste matrici invertibili

Ora che sappiamo che lavorare con matrici in forma di scaglione rende davvero molto più facile risolvere le equazioni di matrici, dovremmo chiederci, quali sono le matrici invertibili $E_1, E_2, ..., E_n$ che renderanno $\tilde A$ in forma di scaglione.

Come funziona l'eliminazione gaussiana?

È interessante notare che non è difficile trovare queste matrici $E_1, E_2, ..., E_n$, che saranno chiamate matrici elementari.

Passo 1 : Guarda la prima colonna, se ha un valore diverso da zero, quello sarà il tuo pivot. Se la prima riga della prima colonna è diversa da zero, usala come pivot. In caso contrario, trova una riga che ha un valore diverso da zero e permuta quella riga e la prima riga.

Quindi, trovi un pivot e potenzialmente devi fare una permutazione di riga (che in realtà è rappresentata moltiplicando per una certa matrice invertibile)

Passo 2 : Una volta che hai un pivot, elimina tutti gli elementi nella colonna corrente, sotto il pivot.

Questo viene fatto moltiplicando la riga pivot per una certa costante e aggiungendola a una riga sotto il pivot, in modo che l'elemento nella stessa colonna del pivot venga azzerato.

Passaggio 3 : Una volta che tutti gli elementi sotto il pivot sono stati azzerati effettuando le operazioni di riga appropriate (che sono rappresentate dall'operazione di una matrice invertibile), spostati alla colonna successiva, riga successiva e cerca un pivot dalla riga sottostante della riga del perno precedente ed eseguire la stessa procedura.

Passaggio 4 : Ripetere fino a quando non si esauriscono le colonne o la matrice è in forma di scaglioni.

ESEMPIO 2

Utilizzando il pivot e l'eliminazione gaussiana, risolvi il seguente sistema:

RISPOSTA:

Prima di tutto, la matrice associata $A$ e il vettore $b$ sono:

La matrice aumentata $[A|b]$ è

Per risolvere il sistema, dobbiamo passare all'eliminazione gaussiana. Scegliamo il primo pivot, iniziando dalla prima colonna. L'elemento nella prima riga della prima colonna è 1, che è diverso da zero e quindi viene utilizzato come pivot. Usiamo quel pivot (1) per eliminare tutti gli elementi sottostanti:

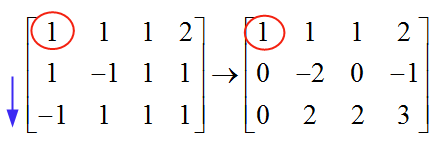
Il meccanismo per eliminare gli elementi sotto il perno è semplice. In questo caso, per eliminare l '"1" che è sotto il pivot, sottraggo gli elementi della riga 1 agli elementi della riga 2. In questo modo formo uno zero sotto il pivot.

Allo stesso modo, per eliminare il "-1" che è nella riga 3, aggiungo gli elementi nella riga 1 agli elementi nella riga 3. In questo modo formo uno zero sotto il pivot nella riga 3.

Vedremo che queste operazioni di riga sono ottenute moltiplicando per matrice invertibile, quindi abbiamo sistemi equivalenti in questo modo.

Ora, passando alla riga successiva, alla colonna successiva, troviamo un "-2", che è diverso da zero, e quindi viene utilizzato come nostro perno. Per eliminare il valore sotto questo pivot, aggiungiamo alla riga 3 i valori della riga 2:

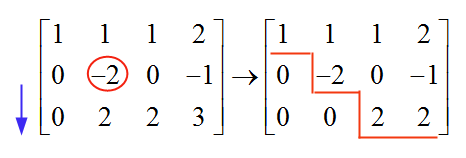
e ora ci fermiamo, perché la matrice risultante è già in forma di scaglione. Ora torniamo indietro per risolvere il sistema: