Maggiori informazioni su questo generatore di grafici quadratici

Questo calcolatore grafico quadratico ti consentirà di generare il grafico per qualsiasi funzione quadratica che fornisci. Può essere qualsiasi funzione quadratica valida, ad esempio x^2 - 3x + 1/2, ma puoi anche fornire una funzione quadratica non semplificata, come x^2 - 3x - 4 - 1/2 x^2 - 1/5, a condizione che sia una funzione quadratica valida.

Dopo aver fornito un'espressione quadratica valida, puoi fare clic sul pulsante "Calcola" e il file grafico della funzione verrà generato, mostrandoti i passi del calcolo del vertice della parabola e il Asse di simmetria anche .

Le funzioni quadratiche hanno un ruolo predominante nell'algebra di base, poiché sono spesso utilizzate nel contesto della soluzione equazioni quadratiche e problemi applicativi. Sono essenzialmente di base polinomio , che hanno molte proprietà interessanti.

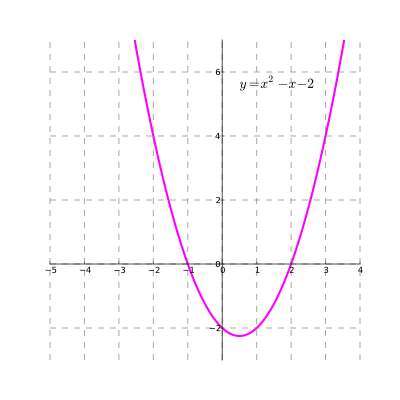
Come rappresentare graficamente le quadratiche?

Fare un grafico quadratico è semplice, nel senso che sai che TUTTE le funzioni quadratiche avranno la forma di una parabola. Eppure ci sono infinite parabole. Abbiamo bisogno di saperne un po' di più per identificare LA parabola precisa che rappresenta una data funzione quadratica.

Passi per trovare un grafico di funzione quadratica

• Passaggio 1: identificare chiaramente la funzione quadratica data e semplificare se necessario
• Passo 2: Dopo aver semplificato, identifica la funzione nella forma f(x) = ax² + bx + c. Si noti che a non può essere zero
• Step 3: Se a > 0, sai che il grafico sarà una parabola che si apre verso l'alto, mentre se a < 0, sai che il grafico sarà una parabola che si apre verso il basso
• Passaggio 4: l'asse di simmetria è in x* = -b/(2a), che indica il "centro" della parabola
• Passaggio 5: notare che x* = -b/(2a) è la coordinata x del vertice della parabola e y* = f(x*) = a(x*)² + b(x*) + c è la coordinata y del vertice

Questo dovrebbe essere sufficiente per avere un'idea chiara del corrispondente grafico quadratico. Un ulteriore passo sarebbe tracciare alcuni punti sul grafico, scegliendo diversi punti dell'asse x e trovando la loro immagine corrispondente attraverso la funzione, così da aiutare il processo di trovare il grafico della funzione .

La formula quadratica

È il formula quadratica relativo al grafico di una funzione quadratica? Scommetti! Geometricamente parlando, quando si risolve l'equazione quadratica

\[a x^2 + bx + c = 0 \]

ottieni le radici dell'equazione quadratica, e quando le radici sono reali, rappresentano i punti in cui la parabola attraversa l'asse x.

Un caso speciale si verifica quando le radici sono complesse, nel qual caso la parabola non attraverserà l'asse x.

Tipi di grafici quadratici

Come accennato in precedenza, TUTTE le funzioni quadratiche univariate saranno rappresentate da parabole, ma a seconda che a > 0 o a < 0, le parabole si apriranno rispettivamente verso l'alto o verso il basso.

Un'altra distinzione dei tipi di parabole potrebbe essere per quelle "centrate" (ovvero, le vertice è l'origine) e quelli che non lo sono.

Esempio: grafico quadratico

Costruisci il grafico di : \(f(x) = \frac{1}{3}x^2 +2x - 3\)

Soluzione:

Dobbiamo rappresentare graficamente la funzione quadratica fornita \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\). Inoltre, verranno calcolate le coordinate del vertice.

Per una funzione quadratica della forma \(f(x) = a x^2 + bx + c\), la coordinata x del vertice viene calcolata utilizzando la seguente formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In questo caso, abbiamo che la funzione per la quale dobbiamo trovare il vertice per è \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\), il che implica che i coefficienti corrispondenti sono:

\[a = \frac{1}{3}\] \[b = 2\] \[c = -3\]

Inserendo i valori noti di \(a\) e \(b\) nella formula per la coordinata x del vertice, otteniamo:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]

Ora, dobbiamo inserire il valore di \(x_V = \displaystyle -3\) nella funzione quadratica, quindi otteniamo:

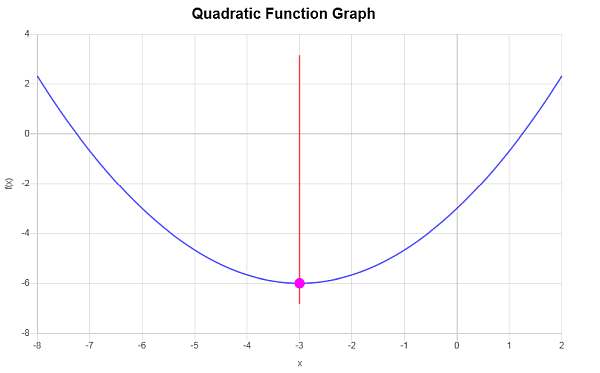
\[y_V = f(x_V)\] \[ = \frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=\frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=9\cdot\frac{1}{3}-6-3=3-6-3=-6\]

Pertanto, la coordinata x del vertice è \(x_V = \displaystyle -3\) e la coordinata y del vertice è \(y_V = \displaystyle -6\). Ciò indica che il punto che rappresenta il vertice è \( \displaystyle \left(-3, -6\right)\).

Graficamente si ottiene:

Esempio: grafico quadratico

Grafico: \(f(x) = \frac{4}{3}x^2 +3x - 2\), che tipo di grafico quadratico è questo?

Soluzione: In questo caso, abbiamo che la funzione per la quale dobbiamo trovare il vertice per è \(f(x) = \displaystyle \frac{4}{3}x^2+3x-2\), il che implica che i coefficienti corrispondenti sono:

\[a = \frac{4}{3}\] \[b = 3\] \[c = -2\]

Inserendo i valori noti di \(a\) e \(b\) nella formula per la coordinata x del vertice, otteniamo:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]

Ora, dobbiamo inserire il valore di \(x_V = \displaystyle -\frac{9}{8}\) nella funzione quadratica, quindi otteniamo:

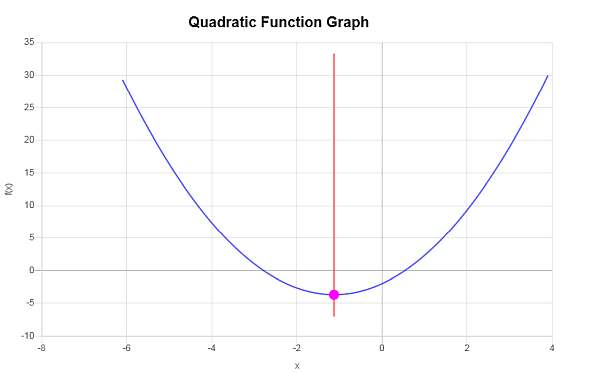
\[y_V = f(x_V)\] \[ = \frac{4}{3}\cdot \left(-\frac{9}{8}\right)^2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]

Pertanto, la coordinata x del vertice è \(x_V = \displaystyle -\frac{9}{8}\) e la coordinata y del vertice è \(y_V = \displaystyle -\frac{59}{16}\). Ciò indica che il punto che rappresenta il vertice è \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).

Graficamente si ottiene:

Altre calcolatrici quadratiche

Quasi tutte le applicazioni in Algebra di base si basano sulla risoluzione di una sorta di Equazione quadrata , quindi ha un forte scopo pedagogico per conoscerlo.

Il formula quadratica è uno degli oggetti insegnabili più famosi in matematica. Non è che le equazioni cubiche o quartiche non esistano, è quello equazioni quadratiche sono quelli che possiamo facilmente spiegare.