Calcolatore di probabilità di poisson

Per saperne di più sul Probabilità della distribuzione di Poisson quindi puoi usare meglio la calcolatrice di Poisson sopra: The Probabilità di Poisson è un tipo di distribuzione di probabilità discreta che può assumere valori casuali nell'intervallo \([0, +\infty)\). Le principali proprietà della distribuzione di Poisson sono:

• È discreto e può assumere valori da 0 a \(+\infty\).


• Il tipo di asimmetria dipende dalla media della popolazione (\(\lambda\))


• È determinato dalla media della popolazione (\(\lambda\))


• La sua media è \(\lambda\) e anche la sua varianza della popolazione è \(\lambda\)

Come utilizzare il calcolatore della distribuzione di poisson

Utilizzando i dati di cui sopra Calcolatore della curva di distribuzione di Poisson , puoi calcolare probabilità della forma \(\Pr(a \le X \le b)\), della forma \(\Pr(X \le b)\) o della forma \(\Pr(X \ge a)\).

Digita il parametro appropriato per \(\lambda\) nella casella di testo in alto, seleziona il tipo di code, specifica il tuo evento e calcola la tua probabilità di Poisson. Osserva che \(\lambda\) corrisponde alla media della popolazione della distribuzione.

Come si calcola la probabilità di poisson?

La formula di distribuzione della probabilità di Poisson è

\[ \Pr(X = k) = \displaystyle \frac{e^{-\lambda} \lambda^k}{k!}\]

Non esiste un'espressione semplice o breve per esprimere il Formula di Poisson cdf , che si ottiene sommando i singoli valori di probabilità fino a un determinato valore di soglia.

Come trovi la probabilità di poisson tra due numeri?

In sostanza, devi valutare la formula di poisson cumulativa (cdf) ai punti finali, che sarebbero i due numeri, diciamo k e m. Ma poiché la distribuzione è discreta, ciò che calcoli è F(m) - F(k-1), dove F è la funzione cdf di Poisson.

Ora, se usi la nostra calcolatrice, non devi preoccuparti di questo, e fornisci solo i due numeri nel modulo qui sopra.

Come calcolare la distribuzione di poisson calcolatrice excel

Excel ha una formula, la formula "=POISSON()" che permette di ottenere sia il pdf che il cdf di Poisson.

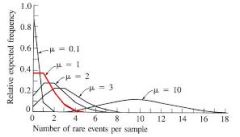
C'è qualche differenza tra la distribuzione di poisson e quella binomiale?

Sì, ci sono chiare differenze. Prima di tutto, non sono la stessa distribuzione. Sebbene siano entrambi discreti (assumano valori che possono essere numerati, come 0, 1, 3, 4, ecc.), presentano alcune differenze fondamentali.

Ad esempio, il Distribuzione di Poisson è determinato da un solo parametro, che è la sua media \(\lambda\). D'altra parte, il Distribuzione binomiale richiede una dimensione del campione N e la probabilità di successo.

Una somiglianza interessante è che entrambe le distribuzioni di probabilità di Poisson e Binomiale possono essere strettamente approssimate con il distribuzione normale in determinate circostanze (dimensione del campione sufficientemente grande).

In effetti, puoi verificarlo con il nostro approssimazione normale per il binomio E approssimazione normale per la distribuzione di Poisson .

Vantaggi di questo calcolatore di poisson

1. Sebbene Excel possa aiutarti con la maggior parte del calcolo delle tue statistiche, questo calcolatore ti mostra tutti i passaggi
2. Vedendo i passaggi, puoi capire meglio il processo di calcolo delle probabilità
3. In definitiva, tutte le distribuzioni discrete seguono la stessa logica per calcolare le probabilità

Esempio: usi di questo calcolatore di probabilità della distribuzione di poisson

Question : Supponiamo che una variabile X abbia una distribuzione di Poisson con media 3.4. Trova la seguente probabilità: \(\Pr(3 \le X \le 6)\).

Soluzione:

Dobbiamo calcolare la probabilità di una distribuzione binomiale. Vengono fornite le seguenti informazioni:

Population Mean \((\lambda)\) =	\(3.4\)
Probability Event =	\(\Pr(3 \le X \le 6) \)

Dobbiamo calcolare \(\Pr(3 \le X \le 6)\). Pertanto si ottiene quanto segue:

\[ \Pr(3 \le X \le 6) = \sum_{i=3}^{ 6} {\Pr(X = i)} = \Pr(X = 3) + \Pr(X = 4) + \Pr(X = 5) + \Pr(X = 6) \] \[ = 0.2186 + 0.1858 + 0.1264 + 0.0716 \]\[= 0.6024 \]

che completa il calcolo.

Altro calcolatore di distribuzione di probabilità discreta

Questo calcolatore di distribuzione di Poisson con passaggi corrisponde a un risolutore per una distribuzione discreta. Abbiamo altri calcolatori di distribuzione discreta che potrebbero interessarti, come il nostro Calcolatrice della distribuzione binomiale , calcolatrice della distribuzione geometrica , e Calcolatrice distribuzione ipergeometrica , per citarne alcuni.

Inoltre, puoi utilizzare il nostro calcolatore di probabilità discreto generale che ti fornirà la media e la deviazione standard di una distribuzione discreta generica.