Calcolatrice della probabilità binomiale

Per saperne di più sul distribuzione binomiale probabilità quindi puoi usare meglio questo calcolatore binomiale: La probabilità binomiale è un tipo di distribuzione di probabilità discreta che può assumere valori casuali nell'intervallo di $[0, n]$, dove $n$ è la dimensione del campione.

Proprietà della probabilità binomiale

Le principali proprietà della distribuzione binomiale sono:

• È discreto e può assumere valori da 0 a n, dove n è la dimensione del campione


• Il tipo di skewness dipende dai parametri n e p


• È determinato da due parametri: la proporzione di successo della popolazione p, la dimensione del campione n (o numero di prove)


• Il media della distribuzione binomiale è $n\cdot p$ e la sua deviazione standard è $\sqrt{np(1-p)}$

Che cos'è la formula della probabilità binomiale?

La formula che definisce la probabilità binomiale (che è chiamata la sua funzione di distribuzione della probabilità ) è:

\[\Pr(X = k) = \left( \begin{matrix} n \\\\ k \end{matrix} p^k \cdot (1-p)^{n-k} \]

dove n e p sono i corrispondenti parametri della distribuzione. Cioè, n è il numero di prove e p è la probabilità di successo di ogni prova.

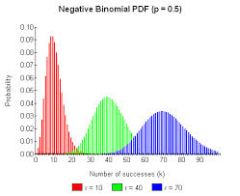
Come utilizzare la calcolatrice per la distribuzione binomiale con i passi necessari

Utilizzando i dati di cui sopra calcolatrice della curva di distribuzione binomiale , siamo in grado di calcolare probabilità della forma $Pr(a \le X \le b)$, della forma $\Pr(X \le b)$ o della forma $\Pr(X \ge a)$. Qualsiasi altro tipo di evento si può derivare da questi tipi elementari di eventi.

Ad esempio, potresti voler trovare la probabilità che X sia compresa tra 0 e 1 o tra 3 e 4. Tale probabilità la calcoleresti come $\Pr(0 \le X \le 1) + \Pr(3 \le X \le 4)$

Digita i parametri appropriati per $n$ e $p$ nella casella di testo in alto, seleziona il tipo di code, specifica il tuo evento e calcola la tua probabilità binomiale, mostrando tutti i dettagli passo passo della formula della probabilità binomiale.

Altri importanti calcolatori di distribuzione di probabilità

La distribuzione binomiale è un tipo di distribuzione discreta. Altre calcolatrici disponibili per le distribuzioni discrete sono le nostre Calcolo della distribuzione di Poisson , calcolatrice ipergeometrica o il nostro calcolatrice della distribuzione geometrica .

Cosa succede quando la probabilità di successo non è costante?

Una forma generalizzata del coefficiente binomiale è il coefficiente di coefficiente multinomiale , che considera combinazioni di numeri $k$ che sommati danno $n$, con $k \ge 2$.

Se si ha a che fare con una distribuzione continua, si consiglia di dare un'occhiata al nostro calcolatore di probabilità normale online , che tratta la distribuzione normale e gli eventi correlati, che è la distribuzione continua più comune.

Esempio: calcolo delle probabilità binomiali

Question : Assumiamo che X sia una variabile casuale con distribuzione binomiale, con parametri n = 10 e p = 0.45. Calcola $\Pr(2\le X\le 4)$.

Soluzione:

Dobbiamo calcolare la probabilità di una distribuzione binomiale. Vengono fornite le seguenti informazioni:

Population Probability of Success $(p)$ =	$0.45$
Sample Size $(n)$ =	$10$
Probability Event =	$\Pr(2 \leq X \leq 4)$

Ciò implica che

$$\Pr(2 \le X \le 4) = \Pr(X = 2) + \Pr(X = 3) + \Pr(X = 4)$$$$= \left( \begin{matrix} 10 \\\\ 2 \end{matrix}\right) 0.45^{ 2} \cdot 0.55^{ 10-2} + \left( \begin{matrix} 10 \\\\ 3 \end{matrix}\right) 0.45^{ 3} \cdot 0.55^{ 10-3} + \left( \begin{matrix} 10 \\\\ 4 \end{matrix}\right) 0.45^{ 4} \cdot 0.55^{ 10-4}$$$$= 0.0763 + 0.1665 + 0.2384$$ $$= 0.4811$$

il che significa che la probabilità che stiamo cercando è $\Pr(2 \leq X \leq 4) = 0.4811$.