La parabole
Une parabole est le lieu géométrique des points des axes de coordonnées qui ont la propriété qu'elles sont équidistantes à partir d'un point fixe (appelé la mise au point) et une ligne (appelée directive).
Je sais ce qui sonne un peu trop technique, mais nous allons passer à travers dessus et, à la fin, vous verrez que ce n'est pas si difficile.
Alors, voudriez-t-il aider si j'ai dit que ça
LA FONCTION \(f(x) = x^2\) REPÉRESENTE UNE PARABOLE?
Bien sûr, cela aidera.Et vous pensez peut-être »Pourquoi vous ne m'avez pas dit dès le début que la parabole est cette fonction?".
Parce qu'il n'y a pas de parabole, il y a un nombre infini d'entre eux.Et une parabole ne doit même pas être représentée par une fonction.Oui, certaines relations sont des parabolas, comme nous le verrons.
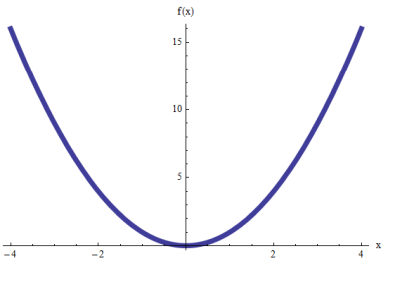
Une chose est importante à mentionner: en utilisant des fonctions et des relations, il existe les parabolas qui "ouverts" le long de l'axe \(y\)-axe, et il y a les parabolas qui "ouvrir" le long de l'axe \(x\).
En fin de compte, par symétrie, il est facile de réaliser que ces parabolas qui "ouvrir" le long de l'axe des Y ont la même structure que ceux qui "ouverts" le long de l'axe des x, il suffit donc d'apprendre à apprendre à apprendre àgérer un type.
L'équation générale de la parabole
Il existe de simples dérivations pour obtenir l'équation d'une parabole basée sur l'emplacement d'une directive et de l'accent, mais nous allons sauter la dérivation dans cette introduction.
Vérifiez le graphique ci-dessous.Nous devons identifier certains éléments cruciaux de la parabole: nous avons le sommet, l'accent et la directive.
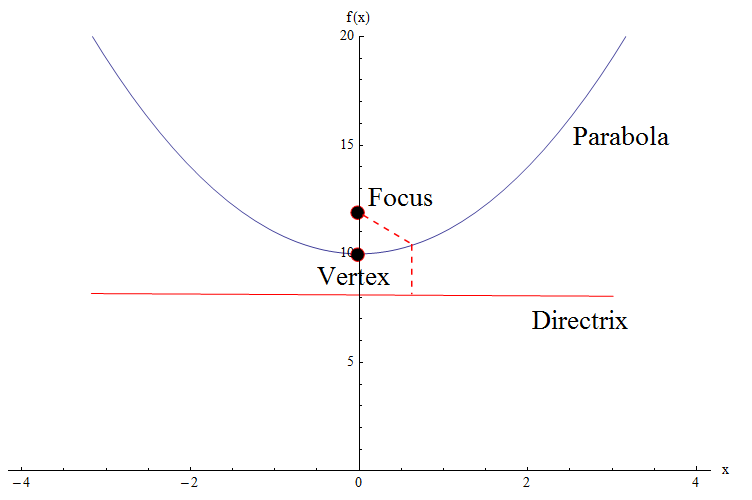
Nous ne ferons pas de détail, mais nous dirons l'équation d'une parabole générale avec sommet à l'origine, avec la mise au point \((0, a)\) et Direcrix égale à \(y = -a\) est
Cette parabole est le genre de parabole qui s'ouvre sur l'axe des Y.
Maintenant, que se passe-t-il lorsque au lieu d'avoir le sommet à l'origine, nous voulons avoir le sommet à un point donné \((k,h)\)?
C'est la magie de travailler avec un système de coordonnées et tout ce que nous devons faire une traduction par le point de point \((k,h)\)?Mais comment faites-vous une traduction de \((k,h)\)?
Simple!Où que vous ayez \(x\), vous le remplacez par \(x-k\), et où vous avez \(y\), vous le remplacez par \(x-h\).
Par conséquent, faire une traduction, l'équation d'une parabole générale avec sommet au point \((k,h)\), avec la mise au point \((k, h+a)\) et Direcrix égal à \(y = h-a\) est
\[\large y-h = 4a(x-k)^2\]qui peut être écrit comme
\[\large \boxed{ y = 4a(x-k)^2 + h }\]Que se passe-t-il avec les parabolas qui s'ouvrent le long de l'axe des x?
Par symétrie, cela a simplement obtenu en remplaçant les rôles de \(x\) et \(y\) dans l'équation de la parabole que nous avons déjà.En praticité, cela signifie que partout où \(x\) apparaît dans l'équation de la parabole que nous avons, nous le changeons \(y\), et inversement pour \(y\).
Par conséquent, l'équation d'une parabole générale avec sommet au point \((h,k)\), avec la mise au point \((h+a, k)\) et la directive égale à \(x = h-a\) est la suivante:
\[\large \boxed{ x = 4a(y-k)^2 + h }\]Notez la différence:
Lorsqu'une parabole a une parabole de la forme \(y = -a\), alors la parabole s'ouvre le long de l'axe des Y (haut ou bas selon que la mise au point est au-dessus ou au-dessous de la directive).
Lorsqu'une parabole a une directive de formulaire \(x = -a\), alors la parabole s'ouvre le long de l'axe des x (gauche ou droite selon que l'accent est mis à gauche ou à droite de la Directrix).
EXEMPLE 1
Trouvez l'équation de la parabole qui a une directive _ xyz _ a _ et un objectif _ xyz_b _.Trouver également le sommet.
RÉPONSE:
Le sommet est sur la parabole, il est donc équidistant à la directive \(y = -4\) et au focus \((0, 4)\), alors le sommet est alors \(0, 0)\).D'autre part, pour une parabole avec sommet à l'origine, l'équation de la directive est \(y = -a\), alors dans ce cas \(a = 4\).Par conséquent, l'équation de la parabole est
\[ \large y = 4ax^2 = 4(4)x^2 = 16x^2 \]Graphiquement:
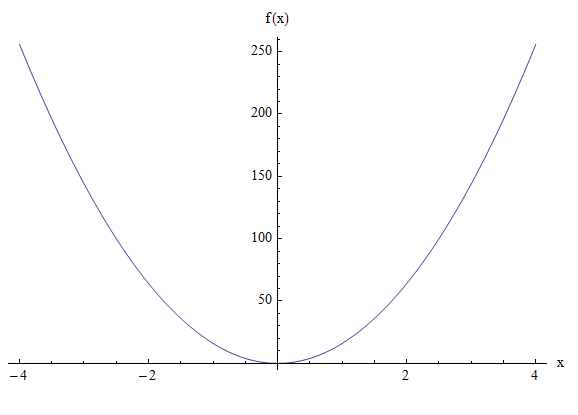
Exemple 2
Trouvez le sommet, la mise au point et la directive du parabola \(y = 8x^2 - 16x + 9\).
RÉPONSE:
Tout d'abord, nous devons compléter la place:
\[\large y = 8x^2 - 16x + 9 = 8(x^2 - 2x) + 9 \] \[\large = 8(x^2 - 2x + 1 - 1) + 9 \] \[\large = 8(x^2 - 2x + 1) + 9 - 8 \] \[\large = 8(x-1)^2 + 1 \]En l'associant à l'équation générale, nous constatons que le sommet est au point \((1, 1)\), et nous avons aussi que \(4a = 8\), donc \(a = 2\), donc la directive est \(y = h - a = 1 - 2 = -1\) et la mise au point est \((k, h + a) = (1, 1+2) = (1, 3)\).
Graphiquement:
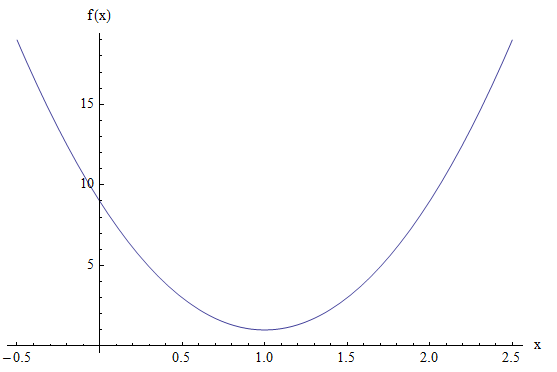
Les sections Parabola et General Conic
Aussi étrange que possible, la parabole est étroitement liée au cône.Comment diriez-vous?Les mathématiciens grecs nommés Apollonius sont du crédit avec une version moderne, utilisant des systèmes de coordonnées, des sections CONic.
Apollonius et d'autres mathématiciens ont découvert que lorsque vous coupez un cône avec un plan, en fonction de l'angle relatif du cône et du plan, le cône est coupé de manière à ce que la section ait différentes formes.
Les différentes formes des sections, en fonction de l'angle relatif de la coupe sont ce que nous savons comme la parabole, le cercle, l'ellipse et l'hyperbole, comme indiqué dans la figure ci-dessous:
En savoir plus sur la parabole
Une parabole générale qui s'ouvre le long de l'axe des Y, avec sommet à l'origine \((0, 0)\) a la représentation fonctionnelle suivante \(y = 4ax^2\).
Ensuite, par symétrie, une parabole générale qui ouvre le long de l'axe des x, avec sommet à l'origine \((0, 0)\) a la représentation fonctionnelle suivante \(x = 4ay^2\).
Ensuite, un sommet général peut être obtenu en appliquant une traduction à un point donné \((k, h)\).
Applications
La parabole a d'innombrables applications en physique, en raison de la manière dont la force de gravité et les lois de Newton fonctionnent, la trajectoire de la plupart des organismes qui sont jetées suivront une trajectoire parabolique.
En outre, algébriquement, les parabolas apparaissent dans l'algèbre tout le temps, car toutes les fonctions quadratiques ont un graphique parabolique et des fonctions quadratiques apparaissent beaucoup dans l'algèbre.
De plus, les parabolas apparaissent dans Calculus lors de la recherche de minima et de Maxima.Il s'avère que de nombreux problèmes de maximisation et de minimisation ont une fonction quadratique permettant de maximiser et géométriquement, le maximum ou le minimum (selon le si le parabola s'ouvre vers le haut ou le bas) est atteint au sommet.
D'autres sections coniques que vous pourriez être intéressées à apprendre sont les ellipse , the hyperbole et le cercer .