Un système d'équations est simplement un ensemble de deux ou plusieurs équations simultanées qui doivent être résolues. En règle générale, vous aurez le même nombre d'équations et d'inconnues (variables), mais ce n'est pas forcément le cas.

La seule chose qui soit claire est que pour avoir un système d'équations, vous devez avoir DEUX équations simultanées ou PLUS. Par exemple, le système ci-dessous

est un système d'équations, avec deux équations et deux inconnues (\(x\) et \(y\)). Ou par exemple, le système ci-dessous:

est un système d'équations, avec deux équations et trois inconnues (\(x\), \(y\) et \(z\)).

Le premier exemple est un exemple de système d'équations linéaires.

Le deuxième exemple est un exemple de système d'équations non linéaires. Pourquoi? Vous l'avez deviné: le terme \(z^2\) dans la première équation le rend non linéaire.

En termes généraux, la stratégie utilisée pour résoudre un système d'équations dépend de son caractère linéaire ou non. Pour les systèmes d'équations linéaires, il existe des méthodes systématiques pour les résoudre, telles que Règle de Cramer . Pour les systèmes d'équations non linéaires, il n'y a pas de stratégie fixe et il faut aller au cas par cas.

Nombre de solutions d'un système d'équations

Combien de solutions un système d'équations a-t-il, le cas échéant? Une réponse générale à cette question ne peut être donnée que dans le cas des systèmes d'équations linéaires, basés sur la relation entre le nombre d'équations et le nombre d'inconnues.

En règle générale, dans un système d'équations linéaires où le nombre d'équations est égal ou supérieur au nombre d'inconnues, il peut y avoir une solution unique, aucune solution ou des solutions infinies.

Lorsque le nombre d'équations est inférieur au nombre d'inconnues, il peut y avoir un nombre infini de solutions, ou pas de solution du tout, mais il ne peut y avoir de solution unique.

Comment trouvez-vous un système d'équations?

Cette question est liée à comment se heurtent à un système d'équations. Il existe plusieurs contextes. Par exemple, vous avez peut-être affaire à un problème de mots, dans lequel vous produisez trois types d'aliments différents, et vous avez plusieurs types de restrictions sur ces aliments en termes de coût, de calories, etc. Chacune de ces restrictions peut probablement être représenté comme une équation.

Il existe d'innombrables applications dans lesquelles différentes restrictions conduisent à des équations linéaires qui doivent être résolues simultanément, convertissant le problème en un système d'équations.

EXEMPLE 1

Exemple de système d'équations: Le système d'équations suivant est-il linéaire ou non linéaire?

RÉPONDRE:

Tout d'abord, ce qui précède est un système d'équations, avec trois équations et trois inconnues (\(x\), \(y\) et \(z\)). Les deux premières équations sont linéaires, que la dernière équation soit non linéaire, en raison du terme \(\sin(z)\). Pour avoir une équation linéaire, nous devons avoir les inconnues à multiplier uniquement par une constante.

Ainsi, le système d'équations ci-dessus n'est pas linéaire, même si les deux premières équations sont linéaires, la troisième ne l'est pas. Pour un système, il suffit d'avoir une équation pour ne pas être linéaire pour que l'ensemble du système soit non linéaire.

EXEMPLE 2

Supposons que vous produisiez trois types de chemises dans les quantités suivantes: \(x\), \(y\) et \(z\). Le type 1 a un coût de 1 $, le type 2 un coût de 1,2 $ et le type 3 un coût de 1,5 $. En outre, il faut 1 heure pour produire le type 1, 0,5 heure pour produire le type 2 et 0,8 heure pour produire le type 3.

Je sais que j'ai 800 $ à dépenser et 500 heures disponibles. De plus, sur la base de mes estimations de la demande, je souhaite produire un total de chemises de type 1 qui équivaut au total combiné du type 2 et du type 3.

Écrivez un système d'équations basé sur ces restrictions. Ce système est-il linéaire?

RÉPONDRE:

Notez qu'il y a trois inconnues (\(x\), \(y\) et \(z\)), ce qui correspond au nombre de chemises de chaque type à produire. De plus, nous avons trois équations: une pour le coût, une pour le nombre d'heures disponibles et une pour la restriction du nombre de chemises de type 1 et les autres types.

Les équations suivantes représentent la situation:

En utilisant la convention de laisser tous les termes qui dépendent des inconnues sur le côté gauche, nous réécrivons la dernière équation pour obtenir:

Notez que chaque équation est linéaire, donc le système est un système d'équations linéaires.

Comment résolvez-vous les systèmes d'égalité en général?

Comme il a été mentionné ci-dessus, il n'y a pas une seule stratégie qui conviendrait à tous les cas. Ce n'est que dans le cas de systèmes d'équations linéaires qu'il y aura une stratégie claire et bien définie.

Néanmoins, il existe certaines bonnes pratiques ou étapes à suivre qui peuvent vous aider à résoudre toutes sortes de systèmes d'équations:

Étape 1: Identifiez chaque équation du système

Étape 2: Déplacez d'un côté de l'équation tous les termes qui dépendent des inconnues (généralement vers la gauche), et les constantes de l'autre côté

Étape 3: Simplifiez à la fois le côté gauche (avec les inconnues) et le côté droit (avec les constantes)

Étape 4: Identifiez la structure des équations. Les équations sont-elles linéaires ou non linéaires?

Étape 5: Si toutes les équations sont linéaires, utilisez l'une des méthodes systématiques de résolution de systèmes linéaires (règle de Cramer, substitution, élimination, réduction de Gauss, etc.)

Étape 6: Si au moins une équation est non linéaire, vous pouvez essayer d'utiliser l'approche de substitution, en commençant par l'équation la plus simple.

En savoir plus sur les systèmes d'équations

Le système d'équations apparaît partout en mathématiques, dans toutes les matières. Être capable de résoudre systématiquement des systèmes d'équations se révélera être une compétence cruciale à maîtriser.

Le système le plus typique que vous trouverez est un système d'équations linéaires. Et souvent, vous trouverez des systèmes d'équations linéaires, avec deux équations et deux inconnues. Ces systèmes sont généralement appelés système 2x2 d'équations linéaires.

Représentation graphique du système d'équations

Pour le système 2x2 d'équations linéaires, nous avons l'avantage de pouvoir utiliser une représentation graphique dans les axes coordonnés. Une équation linéaire est représentée par une ligne dans le plan x-y. Graphiquement, la solution d'un système 2x2 est le point d'intersection des deux lignes, le cas échéant.

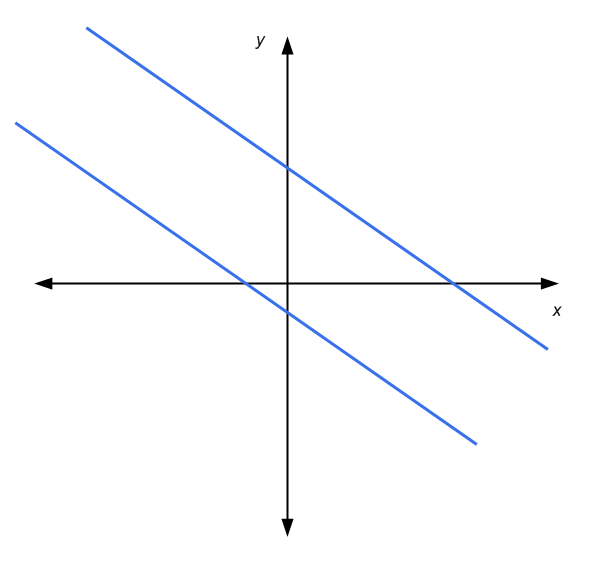
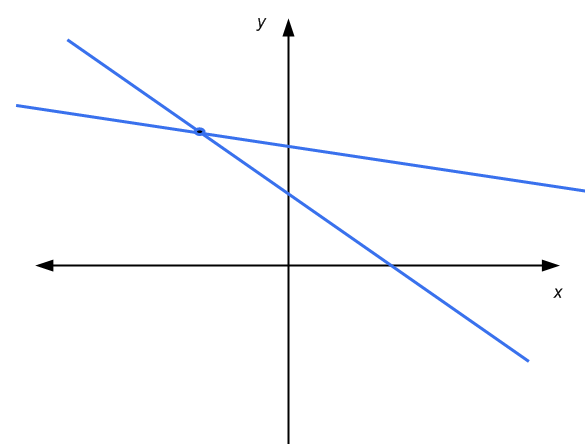
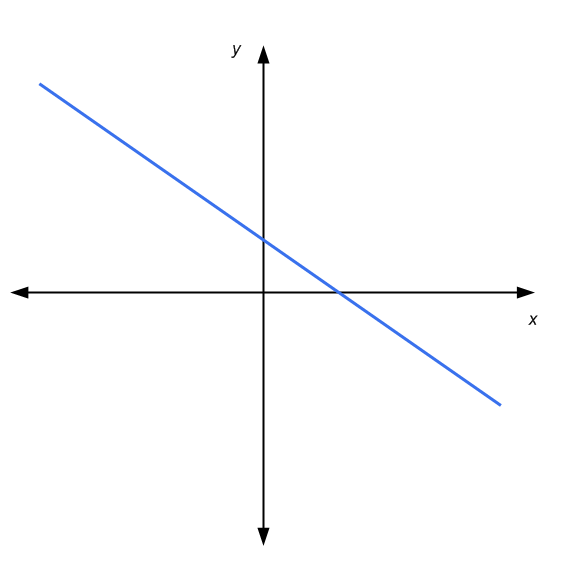
Ensuite, dans ce cas, nous avons soit: les lignes sont parallèles et ne se touchent pas (pas de solutions), les lignes se coupent en un point (solution unique), ou les lignes sont parallèles et se touchent (une infinité de solutions )

Calculatrice de système d'équations

Utilisez ce solveur si vous souhaitez résoudre un système 2x2 d'équations linéaires . Cette calculatrice utilise la règle de Cramer pour résoudre les systèmes 2x2. Pour les systèmes d'équations plus grands, la meilleure alternative est d'utiliser le Méthode d'élimination gaussienne , qui traite systématiquement des systèmes linéaires de toute taille.