Une hyperbole est la place géométrique des points dans les axes de coordonnées qui ont la propriété que la différence entre les distances à deux points fixes (les foyers), est égale à une constante, que nous appelons \(2a\).

Naturellement, cela semble un peu intimidant et trop technique, mais c'est bien la façon dont une hyperbole est définie.

Peut-être que si je vous donne l'équation d'une hyperbole, vous la «reconnaîtrez».

Essayons: c'est l'équation d'une hyperbole très générale:

Pourriez-vous comprendre à quoi il ressemble en vérifiant simplement son équation? Probablement pas. Je vous présente donc l'hyperbole, graphiquement pour vous:

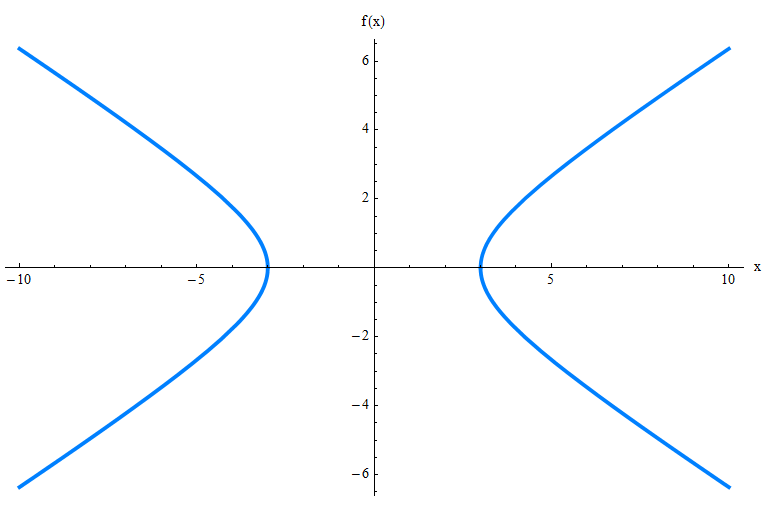
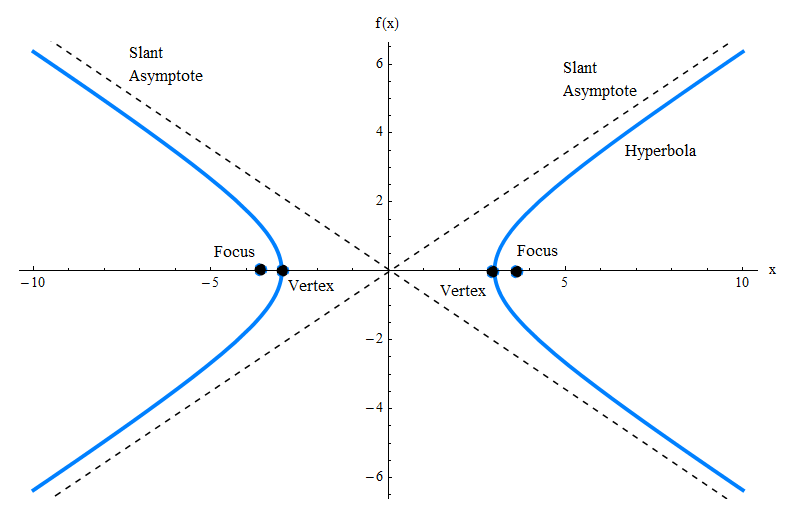
Le graphique ci-dessus ne montre que le graphique de l'hyperbole, mais il y a de nombreux autres éléments dont vous devez être conscient, tels que les asymptotes obliques, les sommets et les foyers. Consultez le graphique ci-dessous.

L'équation générale de l'hyperbole

Sans beaucoup de discussion théorique, nous affirmerons que l'équation générale de l'hyperbole avec des foyers sur l'axe des x est

Pour l'hyperbole décrite par l'équation ci-dessus, elle a des sommets aux points \((-a, 0)\) et \((a, 0)\) et elle a des foyers aux points \((-c, 0)\) et \((c, 0)\), où \(c = \sqrt{a^2 + b^2}\).

Une caractéristique intéressante de cette hyperbole est qu'elle présente deux asymptotes obliques

Asymptote 1 : \(\displaystyle y = \frac{b}{a}x\)

Asymptote 2 : \(\displaystyle y = -\frac{b}{a}x\)

Maintenant que se passe-t-il avec l'équation de l'hyperbole, si au contraire les sommets sont traduits par un point donné \((k,h)\)?

Tout ce que vous avez à faire dans ce cas est de remplacer \(x\) par \(x-k\), et de remplacer \(y\) par \(x-h\).

Par conséquent, en faisant une traduction, nous obtenons que l'équation d'une hyperbole générale est

L'hyperbole ci-dessus a des sommets aux points \((k-a, h)\) et \((k+a, h)\) et elle a des foyers aux points \((k-c, h)\) et \((k+c, h)\), où \(c = \sqrt{a^2 + b^2}\).

Les équations des asymptotes obliques sont \(y = \frac{b}{a}(x-k) + h\) et \(y = -\frac{b}{a}(x-k) + h\).

Que se passe-t-il avec les hyperboles qui s'ouvrent le long de l'axe y?

Par symétrie, il suffit de remplacer simplement les rôles de \(x\) et \(y\) dans l'équation générale de l'hyperbole que nous avons déjà. En pratique, cela signifie que partout où \(x\) apparaît dans l'équation de la parabole que nous avons, nous le changeons \(y\), et vice versa pour \(y\).

Ainsi donc, dans le cas d'une hyperbole qui ouvre longtemps l'axe des abscisses, l'équation générale est

L'hyperbole ci-dessus a des sommets aux points \((k, h - b)\) et \((k, h+b\) et elle a des foyers aux points \((k, h-c)\) et \((k, h+c)\), où \(c = \sqrt{a^2 + b^2}\).

Les équations des asymptotes obliques sont \(y = \frac{b}{a}(x-k) + h\) et \(y = -\frac{b}{a}(x-k) + h\).

EXEMPLE 1

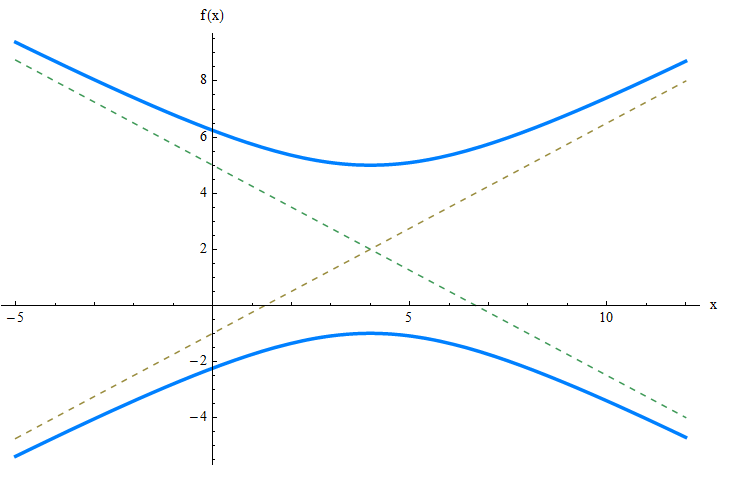
Trouvez les foyers, les sommets et les asymptotes obliques de l'hyperbole:

RÉPONDRE:

Cette hyperbole s'ouvre le long de l'axe y. Dans ce cas, les valeurs de traduction sont \(k = 4\) et \(h = 2\). De plus, nous obtenons que \(a = \sqrt{16} = 4\) et \(b = \sqrt{9} = 3\). Par conséquent, nous obtenons que \(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\).

Par conséquent, les foyers sont \((k, h-c) = (4, 2 - 5) = (4, -3)\) et \((k, h+c) = (4, 2 + 5) = (4, 7)\).

Les sommets sont \((k, h-b) = (4, 2 - 3) = (4, -1)\) et \((k, h+b) = (4, 2 + 3) = (4, 5)\).

Les asymptotes obliques sont

Graphiquement:

EXEMPLE 2

Trouvez l'équation de l'hyperbole avec des foyers au sommet \((-4, 0)\) et \((4, 0)\), focalisation sur \((6, 0\)

RÉPONDRE:

Notez que les foyers et les sommets sont sur l'axe des x, donc l'hyperbole s'ouvre le long de l'axe des x. De plus, puisque les foyers sont symétriques par rapport à l'origine, et qu'un sommet est \((4, 0)\), nous obtenons ce \(a = 4\). Et puisqu'un focus est à \((6, 0)\), nous obtenons ce \(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\).

Par conséquent, l'équation de l'hyperbole est:

L'hyperbole et les sections coniques générales

Comme dans le cas de la parabole, l'hyperbole est étroitement liée au cône. En effet, un mathématicien grec nommé Apollonius est celui qui a découvert cette connexion, en comprenant le concept de sections coniques.

Une section conique se produit lorsque vous coupez un cône avec un plan, et en fonction de l'angle relatif du cône et du plan au point de coupe, le cône est coupé de manière à ce que la section transversale ait une forme spécifique .

Ainsi, en fonction de l'angle de coupe relatif, nous avons différentes formes de section, et ce sont la parabole, le cercle, l'ellipse et l'hyperbole. Voir le graphique ci-dessous: