L'ellipse
Une Ellipse est le lieu géométrique des points dans les axes de coordonnées qui ont la propriété que la somme des distances d'un point donné de l'ellipse à deux points fixes (les foyers) est égale à une constante, que nous appelons \(2a\).
Le concept de «lieu géométrique» est très attrayant d'un point de vue conceptuel, mais il peut ne pas vous donner une vision claire de ce que vous essayez de représenter.
Essayez de faire l'exercice de regarder l'équation ci-dessous et voyez si vous pouvez comprendre à quoi elle ressemble graphiquement;
Pourriez-vous comprendre comment le graphique en regardant simplement l'équation ci-dessus. J'ai pensé ainsi. Laissez-moi vous présenter l'ellipse:
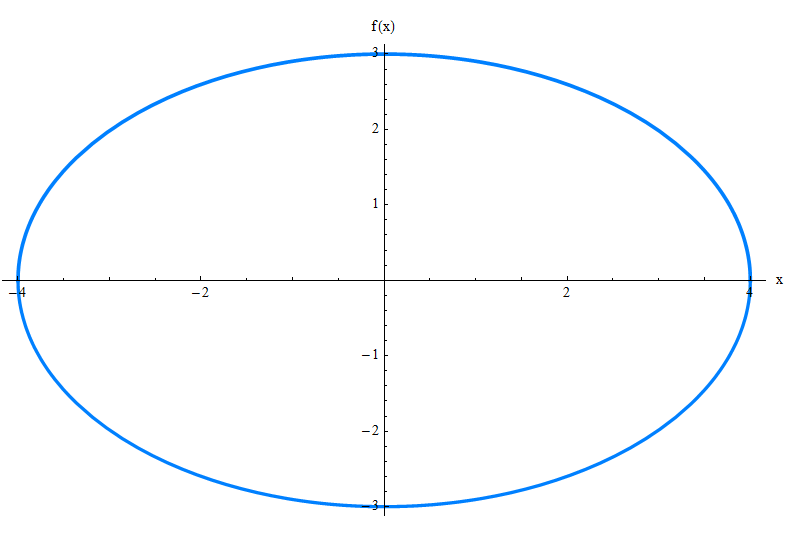
L'équation générale de l'ellipse
Sans beaucoup de discussion théorique, nous dirons que l'équation générale de l'ellipse avec le centre à l'origine, et avec les foyers sur l'axe des abscisses, pour \(a \ge b\) est
\[\large \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Pour l'ellipse décrite ci-dessus, elle a des foyers aux points \((-c, 0)\) et \((c, 0)\), où \(c = \sqrt{a^2 - b^2}\).
Que se passe-t-il maintenant avec l'équation de l'hyperbole ci-dessus lorsque \(b > a\)?
Dans ce cas, les foyers sont sur l’heure y, et ils sont \((0, -c)\) et \((0, c)\), où \(c = \sqrt{b^2 - a^2}\).
Maintenant, si nous voulions déplacer le centre vers un point \((k,h)\)?
Tout ce que vous avez à faire dans ce cas est de remplacer \(x\) par \(x-k\), et de remplacer \(y\) par \(x-h\).
Par conséquent, en faisant une traduction, nous obtenons que l'équation d'une ellipse générale est
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} + \frac{(y-h)^2}{b^2} = 1 }\]L'ellipse ci-dessus a un centre à \((k,h)\) et des foyers à \((k-c, h)\) et \((k+c, h)\) où \(c = \sqrt{a^2 - b^2}\) pour \(a \ge b\), et \((k, h-c)\) et \((k, h+c)\) où \(c = \sqrt{b^2 - a^2}\) pour \(b>a\).
EXEMPLE 1
Trouvez les foyers, de l'ellipse:
\[\large \displaystyle \frac{x^2}{9} + \frac{y^2}{16} = 1 \]RÉPONDRE:
Tout d'abord, en se basant sur la structure de l'équation ci-dessus, l'ellipse est centrée à l'origine \((0, 0)\). Notez que le demi-ax majeur est 4, qui est associé à \(9y\), donc les foyers sont sur l’élément y.
De l'équation, nous avons obtenu que \(a^2 = 9\) et \(b^2 = 16\). Nous trouvons que \(c = \sqrt{b^2 - a^2} = \sqrt{16 - 9} = \sqrt 7\). Par conséquent, les foyers sont à \((0, -\sqrt{7})\) et \((0, \sqrt{7})\).
EXEMPLE 2
Trouvez l'équation de l'ellipse centrée sur \((0, 2)\) avec un focus sur \((6, 2)\) et un ax semi-mineur avec une taille de 3.
RÉPONDRE:
Sur la base des informations fournies, \(c = 6 - 0 = 6\). Puisque les foyers sont sur un comme parallèle à l’élément des x, nous obtenons que \(b = 3\) et ensuite \(a = \sqrt{6^2 - 3^2} = \sqrt{27}\)
Par conséquent, l'équation de l'ellipse est:
\[\large \displaystyle \frac{x^2}{27} + \frac{(y-2)^2}{9} = 1 \]L'ellipse et les sections coniques générales
Comme pour le cas de la parabole, de l'hyperbole et du cercle, l'ellipse est liée au cône. Un mathématicien grec ancien nommé Apollonius a découvert ce lien, avec ce qu'on appelle sections coniques .
Une section conique correspond aux formes qui se forment lorsque vous effectuez une coupe à travers un cône avec un plan, et en fonction de l'angle relatif du cône et du plan, la forme de la section transversale change.
En effet, selon l’endroit auquel le cône et le plan se font face, la forme de la section transversale peut être une parabole, un cercle, une ellipse ou une hyperbole. Ceci est illustré dans le graphique ci-dessous:
En savoir plus sur l'ellipse
Pour une ellipse avec l'équation \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2} = 1 \), avec \(a \ge b\), \(a\) est appelé le demi-grand hache et \(b\) est appelé le semi-petit ax.
Maintenant, \(b > a\), cette dénomination est inversée, donc \(a\) serait appelé le demi-petit hache et \(b\) le demi-grand hache.
L'excentricité
L'excentricité d'une ellipse est calculée à l'aide de la formule suivante:
\[\displaystyle e = \sqrt{1 - \left( \frac{b}{a}\right)^2}\]Ce paramètre d'excentricité indique à quel point la forme de l'ellipse s'écarte d'une version symétrique de l'ellipse (qui est le cercle, qui a l'excentricité \(e = 1\)).
Applications
L'ellipse a tellement d'applications. En science, il est élargi utilisé en astronomie. En effet, les planètes décrivent des orbites elliptiques autour du soleil.
Algébriquement, une ellipse ressemble beaucoup à une hyperbole, mais leurs propriétés sont radicalement différentes.
Vous voudrez peut-être également en savoir plus sur la parabole, pour laquelle vous pouvez vérifier ceci Didacticiel . Vous pouvez également consulter notre tutoriel hyperbole . Enfin, vous pouvez également apprendre tout ce qu'il y a à en savoir plus sur le cercle .