Equações literais
Equações literais são equações onde existem símbolos que não são variáveis, mas representam uma constante. Portanto, é como uma equação, mas alguns dos números, em vez de números, são expressos como constantes genéricas.
Neste tutorial, você aprenderá como lidar com equações literais e como operar com elas.
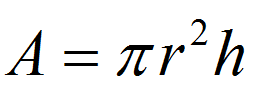
O que é uma equação literal
A primeira tarefa em mãos é especificar o que é uma equação literal. Quando dizemos "literal", estamos nos referindo a "letras". Sim, do latim literal vem de "letras"
Portanto, uma equação literal é uma equação que envolve muitas "letras", ao invés de números. Essas letras não deveriam ser variáveis, deveriam representar números, em termos de uma constante genérica.
Portanto, para identificar uma equação literal, devemos ver muitas letras, das quais uma (ou potencialmente mais) é a
variável
.
Como em qualquer outra equação, a ideia é resolver para a variável (o que significa isolar a variável em um lado da equação).
Por exemplo, considere a fórmula para o volume de um cilindro de raio \(r\) e altura \(h\):
\[V = \pi r^2 h\]Esta é uma equação literal. Por quê? Porque temos uma equação com muitas letras.
A questão é qual é a variável e quais são as constantes. Na verdade, isso é subjetivo, até certo ponto.
Por exemplo, alguém poderia argumentar que \(V\) é a variável e \(r\) e \(h\) são os literais (ou constantes), e isso faria sentido.
Mas pode-se dizer que, por exemplo, recebemos o volume \(V\) e a altura \(h\), e você precisa encontrar o raio \(r\). Nesse caso, temos a mesma equação literal, mas a variável seria \(r\).
É importante saber qual é a variável em uma equação literal, a fim de saber o que estamos resolvendo.
Estratégias para lidar com uma equação literal
Portanto, temos uma equação literal, e agora? Bem, como qualquer outra equação, devemos tentar resolvê-lo.
Isso significa que precisamos isolar a variável de um lado da equação e colocar todo o resto, usando todas as regras algébricas disponíveis, do outro lado.
Isso significa, em termos práticos, que estamos expressando a variável em termos (ou como uma função) das constantes (literais).
O processo de resolução de equações literais é o mesmo que o de resolução de equações regulares:
Adicionamos, subtraímos, multiplicamos ou dividimos os termos em ambos os lados da igualdade para isolar a variável.
Não existe uma forma de resolver, depende das características e da estrutura da equação.
Exemplos de resolução de equações literais
A maneira mais rápida de aprender uma habilidade em matemática é PRATICAR. Aqui vamos nós.
EXEMPLO 1:
Voltemos ao exemplo do cilindro. Para um cilindro com determinado volume \(V\) e altura \(h\), encontre seu raio \(r\)
RESPONDA:
Sabemos que a fórmula para o volume de um cilindro é
\[\large V = \pi r^2 h\]Para a equação literal acima, temos que a variável (aquela que queremos resolver) é \(r\) e as constantes (valores dados) são \(V\) e \(h\).
O processo de resolução de \(r\) é mostrado abaixo:
\[\large V = \pi r^2 h\] \[\large \displaystyle \Rightarrow \frac{V}{\pi h} = r^2\] \[\large \displaystyle \Rightarrow \sqrt{\frac{V}{\pi h}} = r\]Portanto, a equação literal está resolvida, pois temos \(r\) isolado de um lado da igualdade e o restante do outro lado.
EXEMPLO 2:
Resolva a seguinte equação literal:
\[\large m n = \frac{x-y}{k} \]para \(x\).
RESPONDA:
Nesse caso, somos informados explicitamente que a variável é \(x\), então todas as outras letras são constantes para o propósito de resolver a equação.
O seguinte é obtido ao resolver para \(x\):
\[\large m n = \displaystyle \frac{x-y}{k} \] \[\large m n k = x-y \] \[\large m n k+y = x \]que termina o cálculo.
Mais sobre como resolver equações literais
Por que fazemos uma confusão sobre a diferença entre equações literais e equações regulares ?? Na verdade, não fazemos um fuzz. Uma equação literal é uma equação, em primeiro lugar.
O exercício conceitual consiste em perceber que, independentemente de termos um número ou uma constante que representa um número genérico, o processo de resolução da equação é idêntico. Esse é o conceito-chave.
Como resolver equações literais com frações
Então, o que acontece se você encontrar frações ao resolver uma equação literal com frações? Bem, o mesmo que você faria com uma equação regular: se você quiser eliminar algo que está no denominador, você multiplica ambos os lados da equação por ele, e se você deseja eliminar algo que está no numerador, você divide ambos os lados da equação por ele.
Existe alguma estratégia que funcione melhor?
Na verdade não. Dependendo do tipo de equação que você possui, você pode usar algumas estratégias específicas para tornar seu trabalho mais fácil. Por exemplo, se você tiver um equação logarítmica (uma equação em que a variável está dentro de um logaritmo), é melhor fazer um uso eficiente do regras de registro para resolver essas equações de forma eficiente.