Resolvendo equações logarítmicas
Resolver equações logarítmicas é algo que você terá que fazer com frequência ao lidar com os procedimentos algébricos, e vale a pena desenvolver uma estratégia concreta para lidar com eles.
O que você aprenderá neste tutorial é as principais estratégias que você precisa seguir para resolver equações logarítmicas.
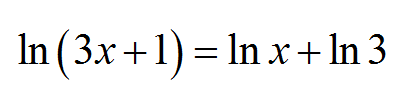
O que é equação logarítmica?
A primeira coisa que precisamos é definir o que é uma equação logarítmica.
Uma equação logarítmica é uma equação que envolve pelo menos uma variável desconhecida, onde uma expressão logarítmica aparece em pelo menos um lado da equação
.
Um exemplo de uma equação logarítmica é
\[\ln x = 2\ln x - \ln 3\]ou também
\[ \ln(3x-1) - \ln(2x + 1) = 1\]
Observe que uma equação logarítmica pode conter mais de um desconhecido, como por exemplo
Estratégias para resolver equações logarítmicas
O primeiro aviso é que não há formas à prova de balas de resolver uma equação logarítmica, nem uma equação geral para esse assunto.A razão para isso é que todos os métodos assumem uma certa estrutura na equação, que não está necessariamente em todas as equações.
Portanto, não podemos encontrar o modo de resolver equações logarítmicas, porque não há sentido de lidar com todos os casos possíveis.
Ainda assim, há algumas estratégias para seguir que lhe dará a melhor chance de passar pela equação e encontrar uma solução, se existir.
Primeiro, tente agrupar toda a expressão logarítmica em uma expressão logarítmica.
Isso é conseguido tipicamente usando o mais comum Regras de log. , que permitem que você compacte uma expressão logarítmica, se a estrutura da expressão permitir isso.
Em segundo lugar, uma vez que as expressões logarítmicas forem compactadas o máximo possível, você se livrará deles, aplicando-se normalmente a função exponencial para os dois lados da igualdade.
Este último passo, espero, removerá todos os logaritmos da imagem, e permitirá que você resolva para o (s) desconhecido (s).
Assim, em outras palavras, resolver uma equação logarítmica consiste em agrupar as expressões logarítmicas, eliminando-as aplicando exponencial e, em seguida, resolver a equação como uma equação regular.
Obviamente, quando você se livrou dos logaritmos, você enfrenta uma equação que poderia ter seus próprios desafios.
Resolvendo diferentes exemplos de equações logarítmicas
Não há melhor maneira de aprender a resolver equações do que realmente praticar resolvê-los:
EXEMPLO 1:
Resolva a seguinte equação:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]RESPONDER:
Vamos seguir as estratégias.A ideia é compactar as expressões logarítmicas, tanto quanto possível.Este é um julgamento, porque a ideia principal é essencialmente se livrar dos logaritmos.
Usando as regras de log, podemos colocar o "4" dentro do logaritmo como
\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]Agora que as expressões logarítmicas são tão compactadas quanto possível, precisamos nos livrar dos logaritmos.
Uma maneira de fazer é aplicar a função exponencial \(10^x\) para cada lado da igualdade.O que quero dizer com isso ???
Bem, você tem dois lados nessa igualdade.Como ambos os lados são os mesmos, quando usados como argumentos da função \(10^x\), deve preservar a igualdade.Então nós temos
\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]Porque sabemos que \(10^{\log a} = a\), que é uma das regras básicas de log.
Então, agora que eliminamos os logaritmos, podemos resolver a equação que resta:
\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]Então, então \(x_1 = 3 + 2\sqrt 2\) e \(x_2 = 3 - 2\sqrt 2\).Tecnicamente, você precisa verificar se essas duas são soluções da equação original, por assim, para garantir que eles pertencem ao domínio das expressões logarítmicas.
Neste caso, ambos \(x_1 = 3 + 2\sqrt 2\) e \(x_2 = 3 - 2\sqrt 2\) são as soluções da equação original.
Exemplo 2:
Resolva a seguinte equação logarítmica:
\[\large \ln 5 - \ln(6-x) = \ln x\]RESPONDER:
Usando as regras de log, podemos compactar as expressões de log, obtemos isso
\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]Porque sabemos que \(e^{\ln a} = a\), que é uma das regras básicas de log.
Portanto, agora que eliminamos os logaritmos, podemos resolver a equação que saímos:
\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]Então, então \(x_1 = 1\) e \(x_2 = 5\).Vamos conectar esses valores na equação original para ver se eles estão de fato soluções:
Para \(x_1 = 1\):
Qual é o mesmo que:
\[\large \ln 5 - \ln(5) = 0\]O que é verdade, então a equação é válida.
Para \(x_1 = 5\):
Qual é o mesmo que:
\[\large \ln 5 - \ln(1) = \ln(5)\]O que é verdade, então a equação é válida.
Portanto, as soluções para a equação são \(x_1 = 1\) e \(x_2 = 5\).
Mais sobre como resolver equações logarítmicas
Uma coisa que os alunos estão mais preocupados é como você se livra do log em uma equação.Mas nós vimos isso é realmente a parte fácil.O que é mais difícil é realmente agrupar a expressão para que os logs possam ser removidos.
Que traz a questão de como lidar com bases diferentes, o que requer seu próprio parágrafo.
Resolvendo equações logarítmicas com bases diferentes
Nos exemplos acima, lidamos apenas com \(\log\) (logaritmo com base 10) e \(\ln\) (logaritmo com base \(e\)).Como você faz quando você tem um logaritmo com uma base diferente, como \(\log_a\) ???
A resposta é simples: a fim de eliminar logaritmos com uma base diferente, diga \(\log_a\) que tem base \(a\) nós simplesmente usamos a função exponencial \(a^x\).Simples direito?
De fato, a eliminação do logaritmo é a parte fácil de resolver equações de log.A parte mais difícil do processo é agrupar e compactar as expressões logarítmicas de uma forma que você os elimine.
Você pode aprender mais sobre como a função logarítmica funciona vendo Como propriedades do SEU Gráficiano e estudando o. REGRAS DE LOG BÁSICAS .