Álgebra Tutoriais

Encontrando o Log Graph

A maneira de encontrar o gráfico log é comum a todas as funções logarítmicas. Isso ocorre porque todas as funções logarítmicas têm essencialmente a mesma forma, pelo menos estruturalmente, ela depende apenas da base do logaritmo.

Primeiro, vamos lembrar a função logarítmica com base \(a\), \(\log_a x\). As bases mais típicas usadas são para \(a = 10\), caso em que escrevemos simplesmente \(\log x\), e o caso em que \(a = e\), caso em que escrevemos \(\ln x\), e o chamamos de log natural.

Por exemplo, o gráfico da função de log natural, \(\ln x\) é mostrado abaixo:

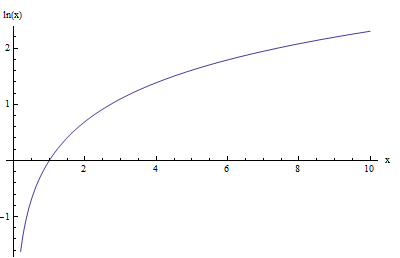
Agora, vamos ver o que acontece quando fazemos o gráfico juntos \(\log x\) e \(\ln x\) (este é o log de base 10 e o log natural):

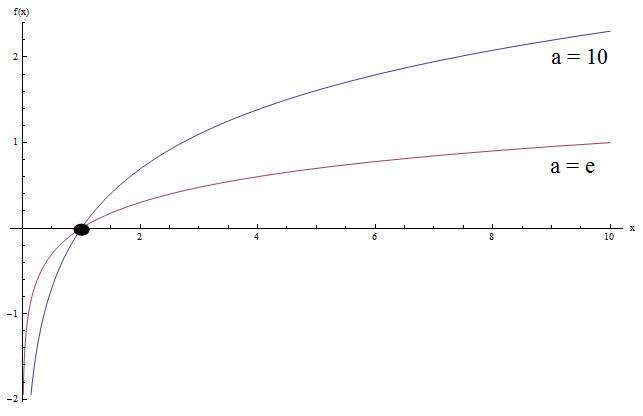
Você vê alguma semelhança? Bem, existem alguns.

Observe que ambos os gráficos têm a mesma forma côncava geral. Além disso, ambos os gráficos cruzam o eixo y em \(x = 1\) (o que não é uma surpresa, pois \(\log_a 1 = 0\) para todas as bases, com \(a > 0\)).

Outra coisa é que ambos os gráficos se aproximam do infinito negativo quando \(x\) se aproxima de 0, e do infinito quando \(x\) se aproxima do infinito.

E se tentarmos representar graficamente as funções logarítmicas com \(0 < a < 1\) ?. Veja o exemplo abaixo:

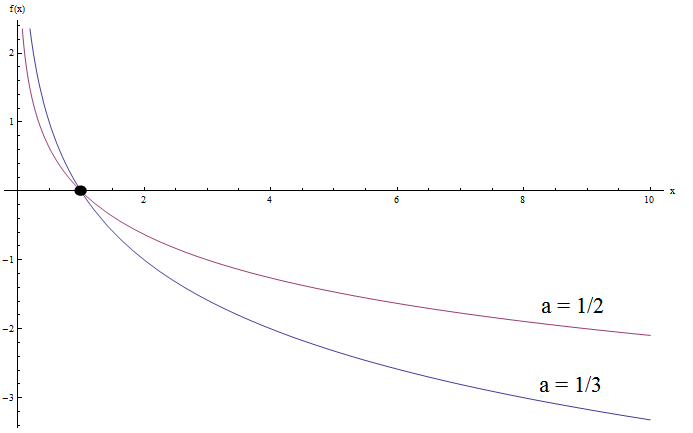
Funções de registro com base inferior a 1

Você vê alguma semelhança agora? Claro.

Observe que ambos os gráficos têm a mesma forma convexa geral. Além disso, ambos os gráficos cruzam novamente o eixo y em \(x = 1\), o que é esperado.

Mas agora ambos os gráficos se aproximam do infinito quando \(x\) se aproxima de 0, e do infinito negativo quando \(x\) se aproxima do infinito. É o comportamento oposto de quando a base \(a\) é maior que 1.

Como você faz um gráfico de registro?

Com base no que encontramos nos exemplos anteriores, podemos adicionar algumas regras que você pode usar quando quiser fazer gráficos de registro:

Suponha que você deseja representar graficamente a função \(y = \log_a x\), para \(a > 0\). Então:

Passo 1 : SEMPRE, a função logarítmica cruza o eixo y em \(x = 1\).

Passo 2 : Se \(a > 1\), então o gráfico é crescente e côncavo. Além disso:

\[\lim_{x\to 0^+} \log_a x = -\infty, \,\, \lim_{x\to \infty} \log_a x = \infty\]

etapa 3 : Se \(0 < a < 1\), então o gráfico é decrescente e convexo. Além disso:

\[\lim_{x\to 0^+} \log_a x = \infty, \,\, \lim_{x\to \infty} \log_a x = -\infty\]

Fácil, certo ??

Mais sobre gráficos de registro

Em primeiro lugar, saber como representar graficamente uma função é uma habilidade crucial, considerando que o gráfico de uma função fornece MUITAS informações sobre ele.

Nas seções anteriores, aprendemos como a base de um registro afeta o gráfico. O interessante é que a forma e o comportamento do gráfico logarítmico dependem apenas de \(a > 1\) e \(0 < a < 1\).

Um log pode ser igual a um número negativo?

Bem, precisamos especificar o que queremos dizer com isso. Primeiro, a base da função logarítmica não pode ser negativa. Além disso, o argumento de uma função logarítmica também não pode ser negativo.

MAS, o logaritmo de um número pode ser absolutamente negativo. Por exemplo: \(\ln(1/e) = -1\).

Como você representa graficamente as funções de log inverso?

Bem, a primeira coisa que você precisa saber é que o inverso de uma função de log sempre será uma função exponencial.

Portanto, representar graficamente o inverso de uma função de log é tão fácil quanto saber qual é o exponencial correspondente e representá-lo graficamente.

Existem outros métodos também. Você pode desenhar o gráfico de registro original e desenhar um gráfico que seja simétrico a este gráfico de registro fornecido, em relação aos 45 ^o linha reta \(y = x\).

Ou use o gráfico original e altere o valor de \(x\) pelo valor de \(y\).

Este tutorial é orientado para as propriedades gráficas da função logarítmica. Para o definição e regras básicas de log, marque esta .