Como Encontrar Alcance
Aprender como encontrar o intervalo de uma função pode ser muito importante em Álgebra e Cálculo, porque lhe dá a capacidade de avaliar quais valores são alcançados por uma função. Ou seja, permite que você encontre o conjunto de todas as imagens por meio da função
A tarefa de descobrir quais pontos podem ser alcançados por uma função é muito útil. Por exemplo, você pode ter uma função de produção \(q(x)\), que fornece a quantidade de saída obtida para unidades de entrada \(x\).
Gostaríamos de saber quantas unidades de entrada são necessárias para produzir \(b\) unidades de saída. Em outras palavras, precisamos encontrar \(x\) para que \(q(x) = b\), que é outra maneira de perguntar se \(b\) está ou não no intervalo da função \(q(x)\).
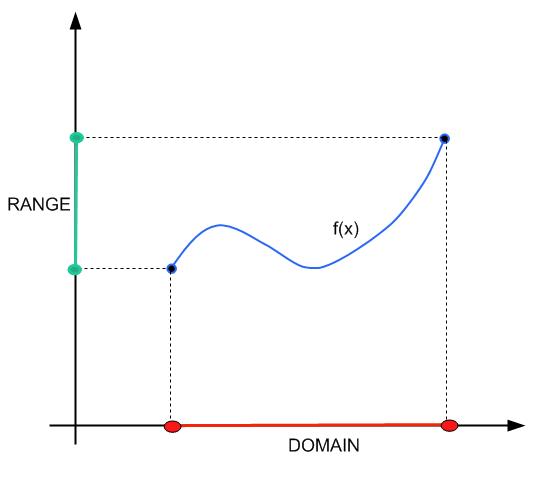
Neste tutorial, vamos nos concentrar mais na mecânica de encontrar o alcance. Para uma abordagem mais conceitual de domínio e alcance, você pode este tutorial .
A maneira algébrica de encontrar o intervalo de uma função
Da mesma forma que quando aprendemos a computar o domínio, não existe uma receita para encontrar o intervalo, realmente depende da estrutura da função \(f(x)\).
No entanto, existe uma técnica algébrica que sempre será usada. Esta é a maneira como você encontra o intervalo. Preste atenção:
Digamos que precisamos obter o intervalo de uma determinada função \(f(x)\). Então, vamos considerar um número real genérico \(y\) e tentaremos resolver para \(x\) a seguinte equação:
\[f(x) = y\]Precisamos determinar para quais valores de \(y\) a equação acima pode ser resolvida para \(x\). É isso. Claro, isso pode ser difícil de fazer, dependendo da estrutura da função \(f(x)\), mas é o que você precisa fazer.
Portanto, esta é a maneira algébrica, a maneira de encontrar o intervalo de uma função sem representar graficamente.
EXEMPLO 1
Encontre o intervalo da função \(\displaystyle f(x) = \frac{x+1}{x-3}\):
RESPONDA:
Prosseguimos usando a maneira algébrica: Seja \(y\) um número e resolveremos para \(x\) na seguinte equação: \(f(x) = y\). O valor \(y\) está no intervalo se \(f(x) = y\) puder ser resolvido para \(x\).
Neste caso, temos:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]Portanto, quando \(x\) estará bem definido? Quase para todos \(y\), exceto quando \(y = 1\), pois nesse caso temos uma divisão por \(0\). Portanto, o intervalo de \(f\) neste caso é toda a linha real, exceto para 1.
Se usarmos a notação de intervalo, podemos escrever \(Range(f) = (-\infty, 1) \cup (1, +\infty)\).
EXEMPLO 2
Encontre o intervalo da função \(f(x) = x^2 - 4x + 3\):
RESPONDA:
Novamente, continuamos usando a maneira algébrica, para que você conheça o procedimento: Seja \(y\) um número e resolveremos para \(x\) na seguinte equação: \(f(x) = y\). O valor \(y\) está no intervalo se \(f(x) = y\) puder ser resolvido para \(x\).
Neste caso, temos:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]Agora, vendo esta expressão final, quando \(x\) estará bem definido? Precisamos ter que o argumento da raiz quadrada precisa ser não negativo, então precisamos:
\[1+y \ge 0\]o que significa que \(y \ge -1\). Se usarmos a notação de intervalo, podemos escrever \(Range(f) = [-1, +\infty)\).
Neste exemplo, poderíamos ter resolvido usando o fato de que \(f(x) = x^2 - 4x + 3\) é uma função quadrática e seu gráfico é uma parábola que se abre para cima.
O ponto mínimo desta parábola é alcançado no vértice. A coordenada x do vértice é:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]Agora, a coordenada y do vértice é simplesmente encontrada inserindo o valor \(x_V = 2\) na função quadrática:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]Como o valor mínimo atingido pela parábola é \(-1\), concluímos que o intervalo é \([-1, +\infty)\), que é a mesma conclusão encontrada algebricamente.
O gráfico da função \(f(x) = x^2 - 4x + 3\) torna ainda mais claro:
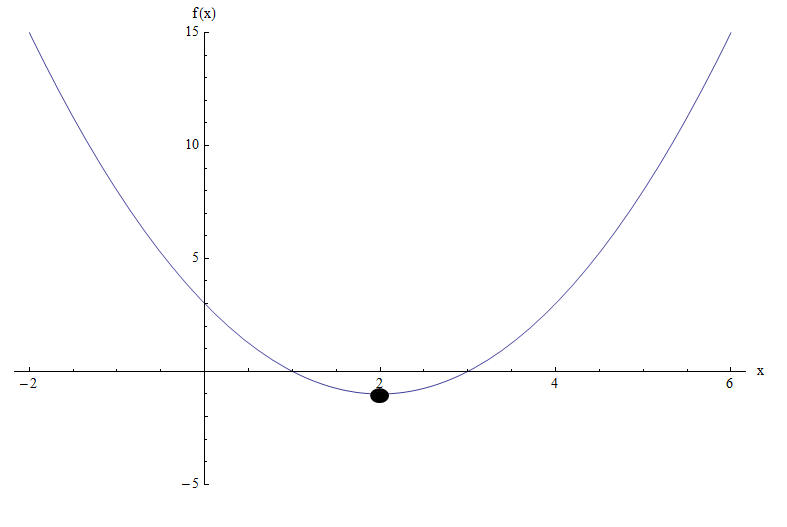
Podemos ver que, com base no gráfico, o mínimo é atingido em \(x = 2\), que é exatamente o que foi encontrado para a coordenada x do vértice.
O risco de usar o gráfico para encontrar o intervalo é que você pode interpretar mal os pontos críticos do gráfico e fornecer uma avaliação imprecisa de onde a função atinge seu máximo ou mínimo.
Outras estratégias para encontrar o alcance de uma função
Como vimos no exemplo anterior, às vezes podemos encontrar o intervalo de uma função apenas olhando seu gráfico.
Por exemplo, digamos que você queira encontrar o intervalo da função \(f(x) = x + 3\). O gráfico é mostrado abaixo:
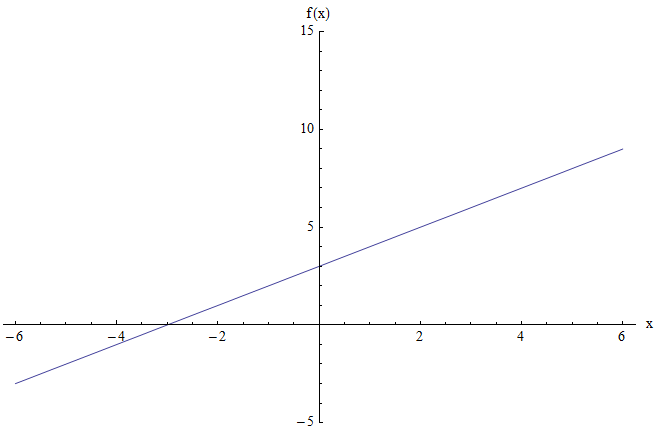
O gráfico acima não mostra nenhum ponto mínimo ou máximo. Além disso, quando \(x\) é grande e positivo, o valor da função também é grande e positivo. E analogamente, quando \(x\) é muito negativo, o valor da função também é muito negativo.
A intuição é que a função pode assumir valores tão negativos e positivos quanto quisermos, selecionando valores \(x\) grandes o suficiente (positivos ou negativos). E então, a conclusão é que o intervalo é toda a reta real, que é \((-\infty, +\infty)\) usando a notação de intervalo.
Tal análise é correta em termos de resultado, mas é frágil em termos de raciocínio. O "método gráfico" para encontrar a faixa tem esse problema: é atraente de um ponto de vista intuitivo, mas é bastante tênue em termos de conteúdo.
Normalmente, se possível, devemos preferir a forma analítica / algébrica. No exemplo, precisamos resolver para \(x\):
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]Então, há alguma restrição em \(y\) para \(x\) ser bem definido? De forma alguma, então, não há restrições em \(y\) e a conclusão é que o intervalo é toda a linha real.
Você pode verificar este artigo que deseja saber como encontrar o domínio de uma função em vez de.
Existem muitas boas razões algébricas para encontrar o intervalo, um deles é porque é uma parte dos processos para encontrar o inverso de uma função .
