Como Encontrar Domínio
Aprender como encontrar o domínio de uma função é uma habilidade crucial em álgebra, porque lhe dá a capacidade de avaliar onde uma função está definida de maneira adequada. Ou seja, a região onde é válido operar a função
A tarefa de descobrir onde é válido operar uma função é útil. Por exemplo, considere a função \(f(x) = \sqrt x\). Sabemos que a função opera valores tais que \(x \ge 0\). Não podemos trabalhar com números negativos, porque obteríamos algo como \(f(-1) = \sqrt{-1}\), que não está bem definido (pelo menos como um número real)
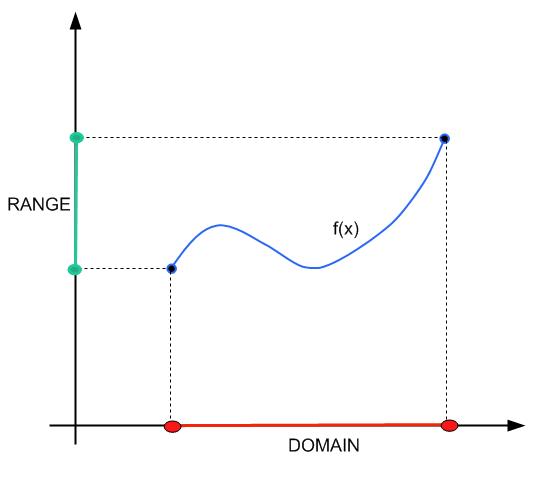
Você pode verificar nosso tutorial anterior, no qual falamos a fundo sobre o Domínio e alcance . Este tutorial será orientado para a parte operacional de encontrar o domínio.
Por que precisamos encontrar o domínio?
A razão pela qual precisamos encontrar o domínio de uma função é que cada função tem um conjunto específico de valores onde é definido. Nem todas as funções são definidas em todos os lugares da linha real.
O domínio a região na linha real onde está válido para trabalhar com a função \(f(x)\), em termos dos valores que \(x\) pode assumir.
O que precisamos fazer para encontrar o domínio?
Na verdade, não existe um truque que sirva para todos os tamanhos. Cada função é diferente e estratégias diferentes precisam ser usadas para encontrar o domínio, dependendo da função.
Existem duas técnicas que você SEMPRE precisa levar em consideração:
Técnica 1
: Certifique-se de que há divisões por zero.
Além disso, aqueles pontos que levam a uma divisão por zero precisam ser excluídos do domínio.
Técnica 2
: Certifique-se de que existem divisões de raízes quadradas com argumentos negativos (como \(\sqrt{-1}\)).
Além disso, aqueles pontos que levam a uma raiz quadrada de um número negativo precisam ser excluídos do domínio.
Em última análise, usando essas duas técnicas, você deve ser capaz de eliminar os pontos que não estão no domínio. Os demais pontos da linha real SÃO parte do domínio, simplesmente.
Portanto, essas duas técnicas resolvem o problema de saber como encontrar o domínio de uma função algebricamente. Outra maneira de fazer isso é olhando o gráfico, se disponível.
EXEMPLO 1
Encontre o domínio da função \(f(x) = \sqrt{x+4}+3\)
RESPONDA:
A primeira coisa que precisamos fazer, e é aí que reside nosso sucesso em encontrar o domínio, é determinar onde podemos encontrar operações inválidas, como divisões por zero ou raízes quadradas negativas.
Para a função \(f(x) = \sqrt{x+4}+3\), não há divisões potenciais por zero, mas há uma raiz quadrada. Para ter um argumento válido, o argumento dentro da raiz quadrada deve ser não negativo.
Portanto, para que \(x\) esteja no domínio da função, precisamos ter \(x\ge 0\). Isso implica que o domínio de \(f\) é \(\{x: x\ge 0\}\) ou \([0, +\infty)\) se usarmos a notação de intervalo.
É sempre assim tão fácil ?? Na verdade não, pode ficar o mais difícil possível, dependendo da complexidade da função \(f(x)\).
Normalmente, porém, os exemplos que você vê em seus testes e trabalhos de casa são bastante simples. Vamos atingir um nível mais alto em termos de dificuldade.
EXEMPLO 2
Agora encontre o domínio da função \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\)
RESPONDA:
Esta função é um pouco mais complexa e requer um tratamento mais cuidadoso. Nesse caso, precisamos nos preocupar com as possíveis divisões por zero e raízes quadradas negativas.
Em primeiro lugar, pode haver uma divisão potencial por zero, quando \(x = 3\), o que indica que \(x = 3\) deve ser excluído do domínio.
Agora, precisamos cuidar de uma raiz quadrada negativa potencial. Precisamos avaliar o sinal de \(\displaystyle \frac{x+4}{x-3}\). Além disso, precisamos que ele não seja negativo, então precisamos resolver:
\[\displaystyle \frac{x+4}{x-3} \ge 0\]Para que uma divisão não seja negativa, precisamos que o numerador e o denominador sejam positivos ou que o numerador e o denominador sejam negativos.
Em outras palavras, precisamos de \(x+4 \ge 0\) e \(x-3 > 0\), ou de \(x+4 \le 0\) e \(x-3 < 0\).
Este é o mesmo que \(x \ge -4\) e \(x > 3\), ou \(x \le -4\) e \(x < 3\).
E isso pode ser escrito como \(x > 3\), ou ambos \(x \le -4\), que corresponde ao intervalo \( (-\infty, -4] \cup (3, +\infty)\).
A conclusão é que o domínio da função \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) é:
\[ dom(f) = (-\infty, -4] \cup (3, +\infty)\]Como você pode ver, o nível de dificuldade aumentou um pouco, e você pode aumentá-lo o quanto quiser.
Como Encontrar o Domínio de uma Função Racional
Em primeiro lugar, lembremos que uma função racional é o quociente de dois polinômios, da forma:
\[f(x) = \frac{p(x)}{q(x)} = \frac{a_0 + a_1 x + ...+ a_m x^m}{b_0 + b_1 x + ...+ b_n x^n}\]Como você encontra o domínio para a função racional acima? Precisamos seguir nossa regra: procure divisões potenciais por zero e raízes quadradas negativas.
Nesse caso, não há raízes quadradas negativas potenciais, mas pode haver divisões por zero, sempre que o polinômio que está no denominador for zero.
A conclusão é muito simples: o domínio de uma função racional é toda a reta real EXCETO para aqueles pontos em que o polinômio no denominador é zero.
EXEMPLO 3
Encontre o domínio de
\[f(x) = \frac{x^2 + x + 1}{x^3 - 6x^2 + 11x - 6}\]RESPONDA:
Primeiramente, precisamos entender que esta é uma função racional, porque você tem dois polinômios \(p(x) = x^2 + x + 1\) e \(q(x) = x^3 - 6x^2 + 11x - 6\) no numerador e denominador, respectivamente.
Então, a primeira etapa é encontrar os zeros do polinômio no denominador, então precisamos resolver: \[ x^3 - 6x^2 + 11x - 6 = 0\]
Essa equação é meio difícil de resolver, então vou dar a você que de fato \(x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3)\), então precisamos resolver:
\[ x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3) = 0\]o que significa que raízes do polinômio no denominador são \(x_1 = 1, x_2 = 2, x_3 = 3\). A conclusão é que o domínio da função é toda a retomada real, exceto para os pontos 1, 2 e 3. Usando a notação de intervalo, o domínio é \((-\infty, +\infty) \backslash \{1,2,3\}\).
Outras estratégias para encontrar o domínio de uma função
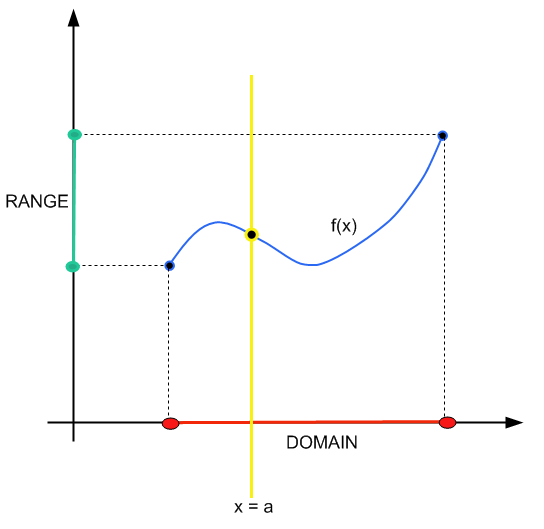
A alternativa de encontrar o domínio de uma função olhando para as divisões potenciais por zero ou raízes quadradas negativas, que é a forma analítica, é olhar para o gráfico.
O método é simples: você constrói uma linha vertical \(x = a\). Se essa linha vertical cruza o gráfico da função em um e apenas um ponto, então \(x = a\) pertence ao domínio.
Curto e grosso.
Finalmente, como você encontra o domínio de uma função com uma raiz quadrada
Este é o cerne de uma das técnicas de que falamos, que são possíveis raízes quadradas negativas. Então, quando você tem uma função com uma ou mais raiz quadrada, sabe que é muito provável que tenha uma raiz negativa potencial e precisa detectá-la.
Porém, nem sempre é esse o caso. Pense na função \(f(x) = \sqrt{x^2}\). Essa função tem uma raiz quadrada, mas o argumento interno é \(x^2\), que não pode ser negativo, então temos um caso de uma função com uma raiz quadrada que não possui raízes quadradas negativas.