Como Encontrar o Inverso de uma Função
Muitas aplicações em Álgebra e Cálculo dependem de saber como encontrar o inverso de uma função, e esse é o tópico deste tutorial.
Em primeiro lugar, você precisa perceber que antes de encontrar o inverso de uma função, você precisa ter certeza de que esse inverso existe.
A coisa boa sobre o método para encontrar o inverso que usaremos é que encontraremos o inverso e descobriremos se ele existe ou não ao mesmo tempo.
Pronto?? Aperte o cinto então.
Como você pode saber se uma função tem um inverso?
Tecnicamente, uma função tem um inverso quando é um-para-um (injetiva) e sobrejetiva.
A condição crucial, porém, é que ele precisa ser um para um, porque uma função pode se tornar sobrejetiva restringindo seu alcance à sua própria imagem.
Como você sabe quando uma função é individual?
Bem, existem pelo menos algumas maneiras. Uma é a forma algébrica e a outra é a forma gráfica (aposto que sei qual você prefere, hein?)
Via Algébrica
Para a forma algébrica, para que uma função \(f\) seja um-para-um, precisamos provar que toda vez que \(f(x) = f(y)\), precisamos ter aquele \(x = y\).
Em outras palavras, precisamos provar que
\[f(x) = f(y) \,\,\Rightarrow \,\, x = y\]
Forma Gráfica
Para a forma gráfica, precisamos usar o teste de linha horizontal : Para qualquer linha horizontal que desenhamos, o gráfico da função cruza no máximo uma vez essa linha horizontal.
Graficamente:
Ele passa no teste da linha horizontal
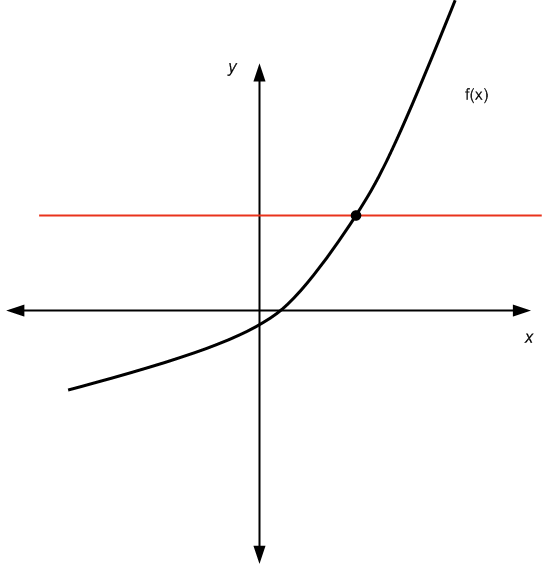
Não passa no teste da linha horizontal
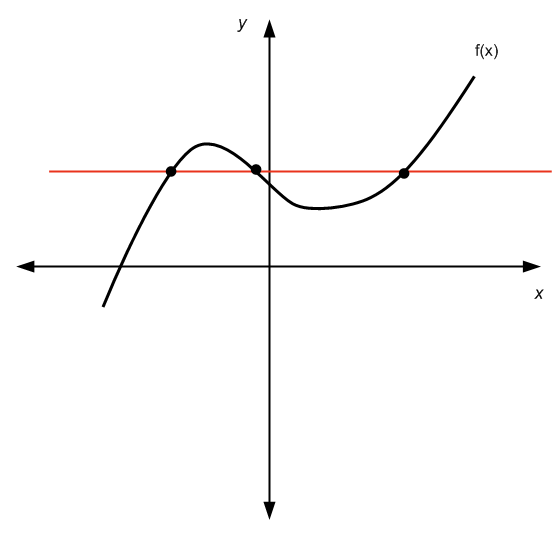
Encontrando o Inverso
Encontrar o inverso de uma determinada função \(f(x)\) requer que você resolva uma equação.
Na verdade, você tem a equação \(f(x) = y\), você toma \(y\) como um determinado número e precisa resolvê-lo para \(x\) e precisa ter certeza de que a solução é ÚNICA.
Isso é tudo. Fácil, certo ??
Agora, para as etapas práticas:
Passo 1:
Para um dado \(y\), defina a equação:
e resolva para \(x\).
Passo 2:
Certifique-se de prestar atenção para ver para qual \(y\), existe realmente uma solução que é única.
Etapa 3:
Depois de resolver \(x\) em termos de \(y\), aquela expressão que depende de \(y\) será seu \(f^{-1}(y)\).
Passo 4:
Mude o nome da variável de \(y\) para \(x\) e você terá sua função inversa \(f^{-1}(x)\).
EXEMPLO 1
Encontre o inverso da função \(f(x) = \sqrt x\)
RESPONDA:
Então, tomamos \(y\) como dado e precisamos resolver \(f(x) = y\), que neste caso corresponde a resolver
\[\sqrt x = y\]Observe que a raiz quadrada é sempre não negativa, portanto, para ter uma solução, precisamos que \(y\ge 0\).
Aplicando o quadrado a ambos os lados, obtemos que
\[\Rightarrow \,\, (\sqrt x)^2 = y^2\] \[\Rightarrow \,\, x = y^2\]Então, \(f^{-1}(y) = y^2\), e trocando o nome da variável, temos a função inversa é
\[f^{-1}(x) = x^2\]para \(x\ge 0\).
EXEMPLO 2
Encontre o inverso da função \(f(x) = \displaystyle \frac{x}{x+1}\), para \(x > -1\)
RESPONDA:
Novamente, consideramos \(y\) como dado e agora precisamos resolver para \(x\) a equação \(f(x) = y\). Então nós temos
\[\displaystyle \frac{x}{x+1} = y\] \[\Rightarrow \,\, x = y(x+1)\] \[\Rightarrow \,\, x = yx + y\] \[\Rightarrow \,\, x - yx = y\] \[\Rightarrow \,\, x(1 - y) = y\] \[\Rightarrow \displaystyle \,\, x = \frac{y}{1-y}\]Então, \(f^{-1}(y) = \displaystyle \frac{y}{1-y}\), e trocando o nome da variável, temos a função inversa é
\[f^{-1}(x) = \displaystyle \frac{x}{1-x}\]Mais sobre como encontrar o inverso de uma função
Uma das propriedades cruciais da função inversa \(f^{-1}(x)\) é que \(f(f^{-1}(x)) = x\).
Pense no que esta coisa está dizendo. Algo como: "A função avaliada no inverso dá a identidade".
Ou em outras palavras, avaliar o inverso por meio da função é como não fazer nada com o argumento.
Ou como algumas pessoas gostam de dizer: A função pode cancelar o inverso de uma forma.
Você escolhe sua versão.
Como encontrar o inverso de uma função quadrática? Você pode?
Na verdade, a resposta é: depende. Isso ocorre porque se considerarmos uma função quadrática em toda a linha real , então não é 1 para 1, pois não passa no teste da linha horizontal, como você pode ver no gráfico abaixo:
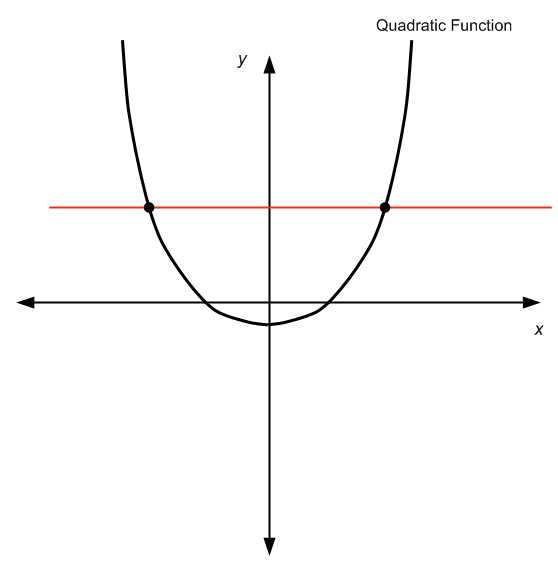
Por não passar no teste de linha horizontal, podemos ver que para um dado \(y\) há mais de um valor \(x\), portanto \(f(x) = y\), portanto não podemos "resolver" para \(x\), pois há mais de um \(x\).
MAS, se você restringir o domínio e considerar dizer apenas os números positivos, obteremos o seguinte:
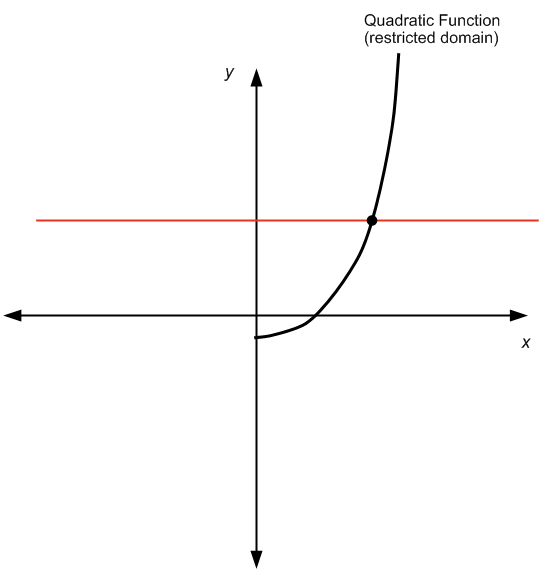
que passa no teste da linha horizontal e, portanto, a função quadrática é invertível.
MORAL DA HISTÓRIA: Para verificar se algo é invertível, NÃO se trata apenas da função. É sobre a função E seu Domínio e alcance .
Como descobrir rapidamente o gráfico de funções inversas
Há sempre a necessidade de avaliar se a função \(f(x)\) é ou não invertível (verificando se é um-para-um ou não). Mas, supondo que você saiba que é invertível, existe uma maneira fácil de encontrar o gráfico do inverso.
Primeiro, represente graficamente a função dada \(f(x)\).
Em seguida, represente graficamente a linha de 45 graus \(y = x\).
Para representar o gráfico de \(f^{-1}(x)\), tudo o que você precisa fazer é refletir o gráfico de \(f(x)\) através da linha de 45 graus \(y = x\), como um espelho.
Veja o exemplo abaixo com as funções \(f(x) = \sin x\) e \(f^{-1}(x) = \arcsin x\)
Outra maneira de ver isso é usar o original gráfico e altere o valor de \(x\) pelo valor de \(y\).
Existe alguma maneira de uma função ser seu próprio inverso?
Sim, é possível, mas só acontece para a função identidade, ou seja, com \(f(x) = x\).