A calculadora de crescimento exponencial

Use esta calculadora de crescimento exponencial para especificar uma função que cresce, fornecendo seu valor inicial e seu crescimento (ou taxa de decaimento). Para fazer uma taxa de crescimento válida, forneça uma taxa positiva.

Além disso, você tem a opção de decidir como essa taxa está agindo, seja anual ou continuamente. Então você clica em "Calcular" para obter todas as etapas mostradas.

O Crescimento Exponencial é um comportamento algébrico que tem muitos usos na vida real, das Finanças à Economia, das Ciências Sociais à Biologia. Representa um crescimento que é composto a cada período por uma determinada taxa (ou percentual).

Uma maneira de ver é que o taxa de variação é proporcional ao tamanho da função.

Fórmula de crescimento exponencial

Diz-se que uma função \(f(t)\) tem um comportamento de crescimento exponencial se puder ser expressa como:

\[f(t) = A_0 (1 + r)^t \]

Para a fórmula acima, \(r\) corresponde à taxa de crescimento, expressa em número decimal ou percentual (são equivalentes).

Normalmente, você receberá a taxa composta de crescimento e o valor inicial \(A_0\), mas às vezes você receberá informações sobre a função e terá que inferir os parâmetros \(r\) e \(A_0\).

Para a fórmula de crescimento exponencial acima, há um caso especial em que a taxa é composta continuamente, caso em que a fórmula se torna

\[f(t) = A_0 e^{rt} \]

Tipicamente, crescimento exponencial As funções representam dinheiro, mas, como mencionamos antes, podem representar uma variedade de fenômenos, como o crescimento populacional.

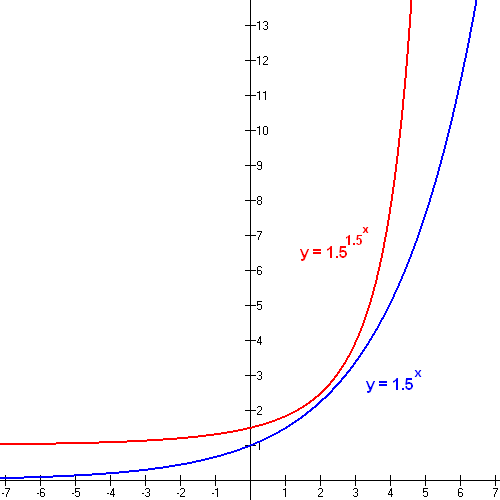
Esse tipo de fenômeno pode ser visto refletido na curva exponencial, que começa relativamente plana, mas aumenta rapidamente.

Aplicações de crescimento exponencial

você pode usar isso Calculadora de função exponencial para diferentes tipos de modelos, desde que conheça os parâmetros necessários.

Um desses modelos típicos envolve populações específicas que crescem rapidamente. Isso pode acontecer com bactérias, insetos e até com a população humana. Normalmente, à medida que as populações crescem rapidamente, a competição por recursos torna-se acirrada e o crescimento deixa de ser exponencial.

Observe que esta calculadora também fornecerá o gráfico da função exponencial resultante.

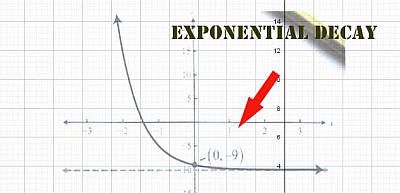
Como o crescimento exponencial e o declínio exponencial estão relacionados?

Crescimento exponencial e decaimento exponencial são absolutamente análogos, e a principal diferença é que a taxa \(r\) no crescimento exponencial é positiva e negativa no decaimento exponencial.

Você também pode usar isso Calculadora De Decaimento Exponencial para o comportamento exponencial inverso, mas análogo, que corresponde ao decaimento exponencial, onde a taxa de crescimento agora é negativa.

Então, como sei se é crescimento ou decadência? Simples, você apenas olha para a taxa, e se for positiva, então você tem crescimento e se for negativa, você tem decadência.

Tanto a calculadora de crescimento exponencial quanto de decaimento mostrarão todas as etapas, que consistem essencialmente em resolver duas equações simultâneas com duas incógnitas

.

Crescimento exponencial de dois pontos

Agora, você pode querer calcular uma função exponencial de dois pontos por onde se sabe que passa.

Mas, como você encontra a taxa de crescimento exponencial com dois pontos? Você começa com uma equação exponencial genérica na forma \(f(t) = A_0 e^{r t}\). Esta equação tem duas incógnitas que são \(A_0\) e \(k\).

Então, inserindo dois pontos \((t_1, y_1)\) e \((t_2, y_2)\) em \(f(t) = A_0 e^{r t}\), você terá duas equações com duas incógnitas, que serão solucionáveis desde que \(t_1 \ne t_2\), o que faz sentido, porque não queremos dois pontos com o mesma coordenada x.