Il test t per campioni appaiati

Per saperne di più sul t-test per due campioni dipendenti così puoi capire meglio i risultati forniti dal risolutore.

Come si calcola un t-test accoppiato?

Un test t per due campioni accoppiati è un test di ipotesi che tenta di fare un'affermazione sulle medie della popolazione (\(\mu_1\) e \(\mu_2\)). Più specificamente, un t-test utilizza le informazioni del campione per valutare quanto sia plausibile che la differenza \(\mu_1\) - \(\mu_2\) sia uguale a zero.

Il test ha due ipotesi non sovrapposte, l'ipotesi nulla e l'ipotesi alternativa. L'ipotesi nulla è un'affermazione sul parametro della popolazione che non indica alcun effetto, e l'ipotesi alternativa è l'ipotesi complementare all'ipotesi nulla. L'idea del test è valutare se esiste o meno una significatività statistica. Le principali proprietà del test t per due campioni appaiati sono:

• Il test ha richiesto due campioni dipendenti, che in realtà sono accoppiati o abbinati oppure si tratta di misure ripetute (misure prese dagli stessi soggetti)


• Come per tutti i test di ipotesi, a seconda della nostra conoscenza della situazione di "nessun effetto", il test t può essere a due code, a coda di sinistra o a coda di destra


• Il principio principale del test di ipotesi è che l'ipotesi nulla viene rifiutata se la statistica del test ottenuta è sufficientemente improbabile nell'ipotesi che l'ipotesi nulla sia vera


• Il valore p è la probabilità di ottenere risultati del campione estremi o più estremi rispetto ai risultati del campione ottenuti, assumendo che l'ipotesi nulla sia vera


• In un test di ipotesi ci sono due tipi di errori. L'errore di tipo I si verifica quando rifiutiamo un'ipotesi nulla vera e l'errore di tipo II si verifica quando non riusciamo a rifiutare un'ipotesi nulla falsa

Come si calcola manualmente un t-test accoppiato? che formula usi?

La formula per una statistica t per due campioni dipendenti è:

\[t = \frac{\bar D}{s_D/\sqrt{n}}\]

dove \(\bar D = \bar X_1 - \bar X_2\) è la differenza media e \(s_D\) è la deviazione standard campionaria delle differenze \(\bar D = X_1^i - X_2^i\), per \(i=1, 2, ... , n\).

Come utilizzare la formula del test t accoppiato

• Fase 1: Innanzitutto, devi definire quali sono le tue ipotesi nulle e alternative. Le scelte sono a due code, sinistra o destra.
• Passo 2: Quindi, devi specificare il tuo livello di significatività. In genere, sceglierai α = 0,05. Questa è la tolleranza che accetti di commettere un errore di tipo I
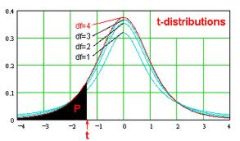
• Smusso 3: In base al livello di significatività che hai scelto e al tipo di coda, trovi le statistiche t critiche guardando una tabella di distribuzione t o usando una calcolatrice o Excel. Quindi, indichi chiaramente la tua regione di rifiuto
• Passaggio 4: Si calcola la statistica t utilizzando la formula specificata sopra t = Dbar/(sd/√n)
• Passaggio 5: Sulla base della statistica t calcolata e se rientra o meno nella regione di rifiuto, si determina se rifiutare o meno l'ipotesi nulla
• Passaggio 6: Usa la conclusione del test t per dare un'interpretazione nel contesto dell'impostazione del problema specifico.

Esempio di test t accoppiato

Question : Si supponga di disporre del seguente campione di dati accoppiati.

	Sample 1	Sample 2	Difference = Sample 1 - Sample 2
	4	2	2
	5	3	2
	6	4	2
	5	5	0
	4	6	-2
	3	4	-1
	5	3	2
Average	4.571	3.857	0.714
St. Dev.	0.976	1.345	1.704
n	7	7	7

L'ipotesi nulla che la differenza media della popolazione sia zero può essere rifiutata al livello di significatività 0,05?

Soluzione:

Dai dati del campione, si trova che le medie campionarie corrispondenti sono:

\[\bar X_1 = 4.571\]\[\bar X_2 = 3.857\]

Inoltre, le deviazioni standard del campione fornite sono:

\[ s_1 = 0.976 \]\[ s_2 = 1.345 \]

e la dimensione del campione è n = 7. Per le differenze di punteggio che abbiamo

\[ \bar D = 0.714 \]\[ s_D = 1.704 \]

(1) Ipotesi nulla e alternativa

Devono essere verificate le seguenti ipotesi nulle e alternative:

\[ \begin{array}{ccl} H_0: \mu_D & = & 0 \\\\ \\\\ H_a: \mu_D & \ne & 0 \end{array}\]

Ciò corrisponde a un test a due code, per il quale può essere utilizzato un test t per due campioni appaiati.

(2) Regione Di Rifiuto

In base alle informazioni fornite, il livello di significatività è \(\alpha = 0.05\) e il valore critico per un test a due code è \(t_c = 2.447\).

La regione di rifiuto per questo test a due code è \(R = \{t: |t| > 2.447\}\)

(3) Statistiche Di Prova

La statistica t viene calcolata come segue:

\[ \begin{array}{ccl} t & = & \displaystyle \frac{\bar D}{s_D/ \sqrt n} \\\\ \\\\ & = & \displaystyle \frac{0.714}{1.704/ \sqrt{7}} \\\\ \\\\ & = & 1.109 \end{array}\]

(4) Decisione sull'ipotesi nulla

Poiché si osserva che \(|t| = 1.109 \le t_c = 2.447\), si conclude che l'ipotesi nulla non è rifiutata.

Utilizzando l'approccio del valore P: il valore p è \(p = 0.31\) e, poiché \(p = 0.31 \ge 0.05\), si conclude che l'ipotesi nulla non è rifiutata.

(5) Conclusione

Si conclude che l'ipotesi nulla Ho non viene rifiutato. Pertanto, non ci sono prove sufficienti per sostenere che la differenza media della popolazione \(\mu_D = \mu_1 - \mu_2\) sia diversa da 0, al livello di significatività \(\alpha = 0.05\).

Intervallo Di Confidenza

L'intervallo di confidenza al 95% è \(-0.862 < \mu_D < 2.291\).

Qual è l'alternativa non parametrica del test t accoppiato?

Questo è un test parametrico che dovrebbe essere utilizzato solo se l'ipotesi di normalità è soddisfatta. Se fallisce, dovresti usare invece this Test dei ranghi con segno di Wilcoxon . Questo calcolatore del t-test accoppiato si occupa della media e della deviazione standard delle coppie.

Altre applicazioni t-test

Spesso hai due campioni che non sono accoppiati, nel qual caso useresti a t-test per il calcolatore di due campioni indipendenti . Si noti che in tal caso i campioni non devono necessariamente avere la stessa dimensione.