Come utilizzare questo calcolatore t-test per un campione

Per saperne di più sul T-test per una media quindi puoi interpretare meglio i risultati ottenuti da questo risolutore: Un test t per una media è un test di ipotesi che tenta di fare un'affermazione sulla media della popolazione (\(\sigma\)). Questo test t, a differenza del test z, non ha bisogno di conoscere la deviazione standard della popolazione \(\sigma\).

Come condurre un test t per la media di una popolazione?

Il test ha due ipotesi complementari, l'ipotesi nulla e l'ipotesi alternativa. L'ipotesi nulla è un'affermazione sulla media della popolazione, nell'ipotesi di nessun effetto, e l'ipotesi alternativa è l'ipotesi complementare all'ipotesi nulla. Le proprietà principali di un test t per un campione per la media di una popolazione sono:

• Per un test t per una media, la distribuzione campionaria utilizzata per la statistica del test t (che è la distribuzione della statistica del test nell'ipotesi che l'ipotesi nulla sia vera) corrisponde alla distribuzione t, con n-1 gradi di libertà (invece di essere la distribuzione normale standard, come nel caso di un test z per una media)


• A seconda delle nostre conoscenze sulla situazione "nessun effetto", il test t può essere a due code, a sinistra oa destra


• Il principio principale del test di ipotesi è che l'ipotesi nulla viene rifiutata se la statistica del test ottenuta è sufficientemente improbabile nell'ipotesi che l'ipotesi nulla sia vera


• Il valore p è la probabilità di ottenere risultati del campione estremi o più estremi rispetto ai risultati del campione ottenuti, assumendo che l'ipotesi nulla sia vera


• In un test di ipotesi ci sono due tipi di errori. L'errore di tipo I si verifica quando rifiutiamo un'ipotesi nulla vera e l'errore di tipo II si verifica quando non riusciamo a rifiutare un'ipotesi nulla falsa

Come calcolare la statistica t per un campione?

Allora, qual è la formula del test t di un campione? In questo caso, per questa formula del test t per la statistica t è

\[t = \frac{\bar X - \mu_0}{s/\sqrt{n}}\]

L'ipotesi nulla è rifiutata quando la statistica t si trova sulla regione di rifiuto, che è determinata dal livello di significatività (\(\alpha\)) dal tipo di coda (a due code, a coda di sinistra o a coda di destra) e dalla numero di gradi di libertà \(df = n - 1\)

Cosa succede con il t-test quando ho 2 campioni

Si noti che questo è un calcolatore di test t di un campione. Se invece devi confrontare due medie, dovresti usare a t-test per campioni indipendenti , Invece.

In modo simile, potresti avere due campioni ma sono accoppiati, abbinati o ripetuti, nel qual caso lo strumento appropriato da utilizzare è questo calcolatore del test t accoppiato , quando è così.

Decisione per un test t di un campione

Come si prende una decisione su un t-test per un campione? Innanzitutto, devi conoscere la statistica t, che chiamiamo \(t_{obs}\), ei gradi di libertà df, in modo da poter calcolare il valore p.

Il processo di calcolo del p-value dipenderà dal tipo di code definito. Per un test a due code, il valore p viene calcolato come \(p = \Pr(|t_{df}| > |t_{obs}|)\). Quindi, per un test con coda di sinistra, il valore p viene calcolato come \(p = \Pr(t_{df} < t_{obs})\) e per un test con coda di destra, il valore p viene calcolato come \(p = \Pr(t_{df} > t_{obs})\).

Un esempio di test t campione

Un venditore ha record che mostrano che il cliente medio spende in media $ 80 dollari nel suo negozio, ma di recente ritiene che tale importo sia aumentato. Raccoglie un campione casuale di n = 30 clienti e scopre che l'importo medio speso per il negozio era di $ 85,4, con una deviazione standard campionaria di $ 12,4. Ha prove sufficienti per affermare che la media spesa per il suo negozio è aumentata in modo significativo, al livello di significatività 0,05?

Soluzione:

Sono state fornite le seguenti informazioni:

Hypothesized Population Mean \((\mu)\) =	\(80\)
Sample Standard Deviation \((s)\) =	\(12.4\)
Sample Size \((n)\) =	\(30\)
Sample Mean \((\bar X)\) =	\(85.4\)
Significance Level \((\alpha)\) =	\(0.05\)

(1) Ipotesi nulla e alternativa

Devono essere verificate le seguenti ipotesi nulle e alternative:

\[ \begin{array}{ccl} H_0: \mu & = & 80 \\\\ \\\\ H_a: \mu & > & 80 \end{array}\]

Ciò corrisponde a un test della coda di destra, per il quale verrà utilizzato un test t per una media, con deviazione standard della popolazione sconosciuta, utilizzando la deviazione standard del campione.

(2) Regione Di Rifiuto

In base alle informazioni fornite, il livello di significatività è \(\alpha = 0.05\) e il valore critico per un test della coda di destra è \(t_c = 1.699\).

La regione di rifiuto per questo test della coda di destra è \(R = \{t: t > 1.699\}\)

(3) Statistiche Di Prova

La statistica t viene calcolata come segue:

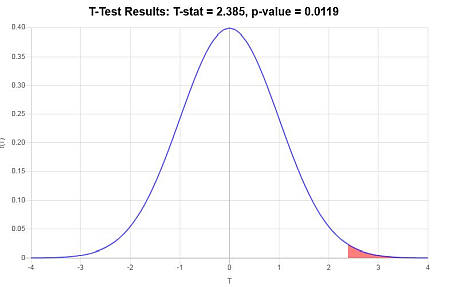
\[ \begin{array}{ccl} t & = & \displaystyle \frac{\bar X - \mu_0}{s/\sqrt{n}} \\\\ \\\\ & = & \displaystyle \frac{ 85.4 - 80}{ 12.4/\sqrt{ 30}} \\\\ \\\\ & = & 2.385 \end{array}\]

(4) Decisione sull'ipotesi nulla

Poiché si osserva che \(t = 2.385 > t_c = 1.699\), si conclude che l'ipotesi nulla è respinta.

Utilizzando l'approccio del valore P: il valore p è \(p = 0.0119\) e, poiché \(p = 0.0119 < 0.05\), si conclude che l'ipotesi nulla è rifiutata.

(5) Conclusione

Si conclude che l'ipotesi nulla Ho viene rifiutato. Pertanto, non ci sono prove sufficienti per sostenere che la media della popolazione \(\mu\) sia maggiore di 80, al livello di significatività \(\alpha = 0.05\).

Intervallo Di Confidenza

L'intervallo di confidenza al 95% è \(80.77 < \mu < 90.03\).

Graficamente