Calcolatrice z-test a due medie

Questa calcolatrice permette di eseguire un test z per due medie, mostrando tutti i passaggi. Il test z è molto simile a a prova t , ma con la netta differenza che per il caso di a Test Z dobbiamo conoscere la corrispondente deviazione standard della popolazione.

Per questo test è necessario fornire due campioni, più la corrispondente deviazione standard della popolazione per ciascun gruppo. Forse ti starai chiedendo cosa succede se non ho quelle deviazioni standard della popolazione: la risposta è semplice: quindi NON PUOI eseguire il test z per due medie.

Una volta forniti tutti i dati richiesti, non dovrai fare altro che cliccare su "Calcola", e ti verranno mostrati tutti i passaggi del processo.

Che cos'è un test z a due campioni?

Uno z-test a due campioni è un tipo di z-test che confronta le medie di due gruppi. È possibile fornire i dati di esempio (insieme alle deviazioni standard della popolazione) oppure eseguire a z-test per due medie con dati riepilogati , per cui è necessario fornire i mezzi di esempio al posto dei dati di esempio.

Quale dei due processi eseguirai, il test z per i dati di esempio o per i dati riepilogati dipenderà in gran parte dalle informazioni che hai a disposizione.

Z-test per due formule medie

C'è una semplice espressione per la formula usata in questo test. La formula del test z è

$$z = \displaystyle{\frac{\bar X_1 - \bar X_2}{\sqrt{\displaystyle{\frac{\sigma_1^2}{n_1}} + \displaystyle{\frac{\sigma_2^2}{n_2}} }}}$$

Il vantaggio in questo caso è che non abbiamo bisogno di occuparci dei gradi di libertà, come nel caso del t-test per due medie , e con i test t in generale.

Come eseguire un test z di 2 campioni su questa calcolatrice?

• Passo 1: Identifica i campioni che desideri confrontare. Di solito, ti piacerebbe condurre alcune analisi statistiche descrittive per assicurarti che i campioni siano ragionevolmente a forma di campana
• Passo 2: È inoltre necessario identificare le deviazioni standard della popolazione $\sigma_1$ e $\sigma_2$. Se non li hai, non puoi eseguire uno z-test
• Passaggio 3: Dai campioni, devi trovare il campione significa $\bar X_1$ e $\bar X_2$
• Passaggio 4: Ora inserisci le tue informazioni nella formula $z = \displaystyle{\frac{\bar X_1 - \bar X_2}{\sqrt{\displaystyle{\frac{\sigma_1^2}{n_1}} + \displaystyle{\frac{\sigma_2^2}{n_2}} }}}$
• Passaggio 5: Una volta che hai la statistica z, che chiami $z_{obs}$ devi calcolare il valore p
• Passaggio 6: Per i test a coda di sinistra si calcola $p = \Pr(Z < z_{obs})$. Per i test a coda di destra si calcola $p = \Pr(Z > z_{obs})$ e per i test a due code si calcola $p = \Pr(|Z| > z_{obs})$
• Passaggio 7: Una volta che hai il p-value, fai una conclusione basata sul valore scelto del livello di significatività $\alpha$: se $p < \alpha$, respingi l&#39;ipotesi nulla, altrimenti non hai prove sufficienti per rifiutare l&#39;ipotesi nulla ipotesi

Un punto importante: se non rifiuti l&#39;ipotesi nulla Ho, ciò non significa che accetti l&#39;ipotesi nulla, significa solo che non hai trovato prove sufficienti per rifiutarla.

In che modo è diverso dal test z per due proporzioni?

sono simili nel senso che sono entrambi z-test, che usano il distribuzione normale determinare tutte le probabilità associate.

La differenza è che stanno misurando cose diverse: il test z per due medie confronta le medie di due gruppi, dove queste variabili sono misurate a livello di intervallo o rapporto, mentre il test z per due proporzioni confronterà la proporzione di un determinate caratteristiche associate ai dati.

Come eseguire un test z a due campioni in excel?

Excel ha funzioni interne che ti consentono di eseguire uno z-test e molte altre procedure, ma non ti mostra tutti i passaggi del processo come fa questa calcolatrice.

Alla fine, potresti essere in grado di ottenere una risposta numerica da Excel o da un&#39;altra calcolatrice, ma non avrai i passaggi su come trovare effettivamente il test z su una normale calcolatrice.

Un esempio di due significa z-test

Un istruttore sta testando un metodo di insegnamento e fa sottoporre un campione di 10 studenti a un metodo e un altro campione di 11 studenti all&#39;altro metodo. I voti ottenuti dopo aver insegnato con questi metodi sono:

Gruppo 1: 89, 78, 90, 100, 90, 92, 90, 80, 89, 93

Gruppo 2: 91, 89, 91, 95, 92, 93, 91, 87, 90, 94, 90

Inoltre, sa che la deviazione standard dei punteggi della popolazione per il primo metodo è 3,4, mentre per il secondo è 4,1. L&#39;istruttore può concludere che esiste una differenza significativa tra i metodi? Utilizzare un livello di significatività di 0,05

Soluzione:

Sono state fornite le seguenti informazioni di esempio:

Campione 1	Campione 2
89	91
78	89
90	91
100	95
90	92
92	93
90	91
80	87
89	90
93	94
	90

Per condurre un test z a due campioni indipendenti, dobbiamo calcolare le statistiche descrittive dei campioni:

	Campione 1	Campione 2
	89	91
	78	89
	90	91
	100	95
	90	92
	92	93
	90	91
	80	87
	89	90
	93	94
		90
Media	89.1	91.1818
N	10	11

Riassumendo, nel calcolo della statistica z verranno utilizzate le seguenti statistiche descrittive:

Sono state fornite le seguenti informazioni:

Sample Mean 1 $(\bar X_1)$ =	$89.1$
Population Standard Deviation 1$(\sigma_1)$ =	$3.4$
Sample Size 1$(n_1)$ =	$10$
Sample Mean 2 $(\bar X_2)$ =	$91.1818$
Population Standard Deviation 2 $(\sigma_2)$ =	$4.1$
Sample Size 2$(n_2)$ =	$11$
Significance Level $(\alpha)$	$0.05$

(1) Ipotesi nulla e alternativa

Devono essere verificate le seguenti ipotesi nulle e alternative:

$$\begin{array}{ccl} H_0: \mu_1 & = & \mu_2 \\\\ \\\\ H_a: \mu_1 & \ne & \mu_2 \end{array}$$

Ciò corrisponde a un test a due code e verrà utilizzato un test z per due medie, con deviazioni standard della popolazione note.

(2) Regione Di Rifiuto

In base alle informazioni fornite, il livello di significatività è $\alpha = 0.05$ e il valore critico per un test a due code è $z_c = 1.96$.

La regione di rifiuto per questo test a due code è $R = \{z: |z| > 1.96\}$

(3) Statistiche Di Prova

La statistica z viene calcolata come segue:

$$\begin{array}{ccl} z & = & \displaystyle \frac{\bar X_1 - \bar X_2}{\sqrt{ {\sigma_1^2/n_1} + {\sigma_2^2/n_2} }} \\\\ \\\\ & = & \displaystyle \frac{ 89.1 - 91.1818}{\sqrt{ {3.4^2/10} + {4.1^2/11} }} \\\\ \\\\ & = & -1.271 \end{array}$$

(4) Decisione sull&#39;ipotesi nulla

Poiché si osserva che $|z| = 1.271 \le z_c = 1.96$, si conclude che l'ipotesi nulla non è rifiutata.

Utilizzo dell&#39;approccio del valore P: il valore P è $p = 0.2038$ e, poiché $p = 0.2038 \ge 0.05$, si conclude che l&#39;ipotesi nulla non viene rifiutata.

(5) Conclusione

Si conclude che l&#39;ipotesi nulla Ho non viene rifiutato. Pertanto, non ci sono prove sufficienti per sostenere che la media della popolazione $\mu_1$ sia diversa da $\mu_2$, al livello di significatività $\alpha = 0.05$.

Intervallo Di Confidenza

L&#39;intervallo di confidenza al 95% per $\mu_1-\mu_2$ è $-5.293 < \mu_1 - \mu_2 < 1.129$.

Graficamente

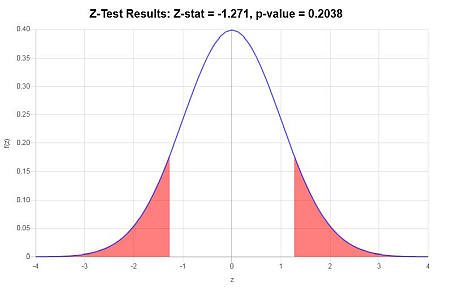
Altri calcolatori di test statistici

Strettamente correlato a questa calcolatrice, hai la calcolatrice per a z-test per due campioni con dati riepilogati , che svolge sostanzialmente la stessa procedura, ma riceve il riepilogo delle statistiche descrittive già note.

All&#39;interno della famiglia di Test Z , abbiamo il test z per una media e il Z-test per due proporzioni .

Inoltre, potresti essere interessato a a calcolatore di frazioni miste , a seconda delle impostazioni di apprendimento. In impostazioni più elementari, i numeri misti sono trattati come entità importanti, mentre in impostazioni più avanzate, i numeri misti sono semplicemente presentati nella loro notazione frazionaria.