Calcolatore del coefficiente di correlazione

Il coefficiente di correlazione calcolato sopra corrisponde al coefficiente di correlazione di Pearson. I requisiti per il calcolo è che le due variabili X e Y siano misurate almeno a livello di intervallo (il che significa che non funziona con variabili nominali o ordinali).

La formula per il coefficiente di correlazione di Pearson è:

\[r =\frac{n \sum_{i=1}^n x_i y_i - \left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{n \sum_{i=1}^n x_i^2 - \left( \sum_{i=1}^n x_i \right)^2} \sqrt{n \sum_{i=1}^n y_i^2 - \left( \sum_{i=1}^n y_i \right)^2} }\]

o equivalente

\[r = \frac{\sum_{i=1}^n x_i y_i - \frac{1}{n}\left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right) }{\sqrt{\sum_{i=1}^n x_i^2 - \frac{1}{n}\left( \sum_{i=1}^n x_i \right)^2} \sqrt{\sum_{i=1}^n y_i^2 - \frac{1}{n}\left( \sum_{i=1}^n y_i \right)^2}} = \frac{SS_{XY}}{\sqrt{SS_{XX}\cdot SS_{YY} }}\]

Se hai due o più variabili, puoi usare our calcolatore della matrice di correlazione . Inoltre, se i dati per le variabili \(X\) e \(Y\) non soddisfano le ipotesi parametriche per la correlazione di Pearson, allora dovresti usare questo Il calcolatore di correlazione di Spearman Invece.

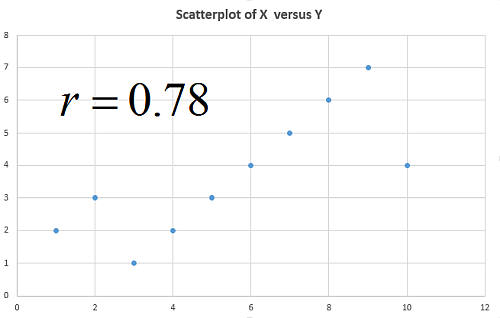
Correlazione e regressione

Correlazione e regressione non sono la stessa cosa, sebbene siano concetti strettamente correlati. L'analisi di correlazione corrisponde al calcolo del coefficiente di correlazione, che è un valore compreso tra -1 e 1, che valuta il grado di associazione lineare tra due variabili.

Quanto più vicino in valore assoluto il correlazione arriva a 1, più stretta è l'associazione lineare tra le due variabili. Vicino a 1 indica un'associazione lineare positiva stretta e vicino a -1 indica un'associazione negativa stretta

Il processo di conduzione di un'analisi di correlazione spesso coinvolge anche costruzione di un grafico a dispersione , al fine di confermare l'informazione fornita dal coefficiente coefficiente.

Una volta confermato che la correlazione è vicina a 1 in valore assoluto e che il grafico a dispersione mostra un modello lineare ragionevolmente stretto, allora possiamo eseguire un Regressione lineare analisi, al fine di valutare quantitativamente l'effetto della variabile indipendente X sulla variabile dipendente Y.

Posso usare i punteggi z per calcolare il coefficiente di correlazione

Certamente! Hai visto punteggi z ovunque in Statistiche e, naturalmente, ti chiedi se puoi calcolare la correlazione con i punteggi z . Puoi sicuramente farlo, e infatti, è il modo consueto di farlo nelle statistiche delle scienze sociali.

Altri calcolatori simili a questo calcolatore di correlazione

Inoltre, c'è il concetto di coefficiente di correlazione multipla , quando si dispone di più di un predittore, ottenuto calcolando la correlazione tra i valori \(Y\) osservati e i valori previsti \(\hat Y\) dalla regressione.