Ulteriori informazioni sulla matrice di correlazione

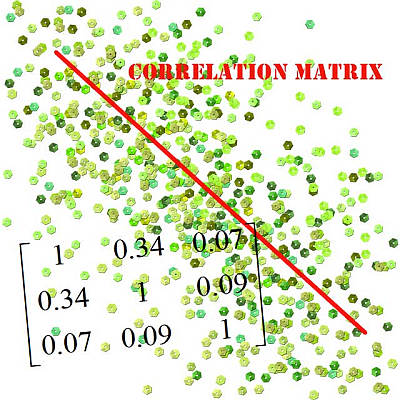
Una matrice di correlazione è una tabella in cui le correlazioni a coppie tra diverse variabili sono opportunamente organizzate in una forma matriciale. Il valore nella i-esima riga e nella j-esima colonna corrisponde alla correlazione tra le variabili \(X_i\) e \(X_j\).

In parole semplici, la matrice di correlazione è un riepilogo di tutte le correlazioni che si possono trovare per un insieme di variabili, per le quali sono disponibili dati campione.

Il calcolo della correlazione è fondamentale, perché è necessario applicare il passaggio precedente a Calcolatrice di regressione lineare per trovare il modello dei minimi quadrati. Ma questo dovrebbe essere tentato solo quando il la correlazione risulta essere significativa .

Formula della matrice di correlazione

Poiché \(corr(X_i, X_j) = corr(X_j, X_i)\), allora la matrice di correlazione è simmetrica, e per tale motivo, per non essere ridondante, la matrice di correlazione riporta solo i valori dalla diagonale in su. Per altre operazioni di correlazione, puoi farlo calcolare un coefficiente di correlazione mostrando tutti i passaggi, oppure puoi usare questo calcolatore di correlazione critica .

Come si calcola una matrice di correlazione

Per capire come calcolare una matrice di correlazione, devi prima sapere come calcolare la correlazione di Pearson, perché la matrice di correlazione è semplicemente la matrice delle correlazioni tra tutte le possibili coppie di variabili.

Per poter procedere con il calcolo della matrice di correlazione è necessario seguire questi passi:

Passo 1: Elenca le variabili che hai, ad esempio X1, X2, ..., ecc. A ciascuna di queste variabili è associato un campione

Passo 2: Prendi le variabili i-esima e j-esima dalla tua lista, Xi e Xj, e calcola il coefficiente di correlazione per esse. Chiamalo \(r_{ij}\)

Passaggio 3: Prendi il valore \(r_{ij}\) e quello sarà il valore della riga i, colonna j della matrice di correlazione

I valori di correlazione vicini a 1 o -1 indicano forti associazioni lineari, suggerendo che a Calcolatrice di regressione lineare (o un regressione lineare multipla , a seconda di quanti predittori hai).

Come si usa una matrice di correlazione?

Questo è un punto che deve essere affrontato, poiché spesso una matrice di correlazione può essere fornita in formati diversi. La matrice di correlazione sarà una tabella con lo stesso numero di righe e colonne, dove il nome delle variabili apparirà nelle righe e nelle colonne corrispondenti.

Quindi, se la prima variabile è \(X_1\), la prima riga ti fornirà il coefficiente di correlazione di \(X_1\) e di ciascuna delle altre variabili. E se la seconda variabile è \(X_2\), la seconda riga ti fornirà il coefficiente di correlazione di \(X_2\) e di ciascuna delle altre variabili, e così via.

In base al modo in cui questo viene definito, nella riga 1, colonna 1 si ha la correlazione di \(X_1\) con se stesso, che è 1, quindi nella riga 2, colonna 2 si ha la correlazione di \(X_2\) con se stesso, che è anche 1 e così via.

Quindi quello che succede è che scoprirai che la diagonale della matrice di correlazione contiene sempre solo 1. Poiché questo è qualcosa che accade sempre, spesso la matrice di correlazione calcolata ometterà la diagonale (perché sappiamo già che contiene 1, quindi che senso ha scriverlo esplicitamente).

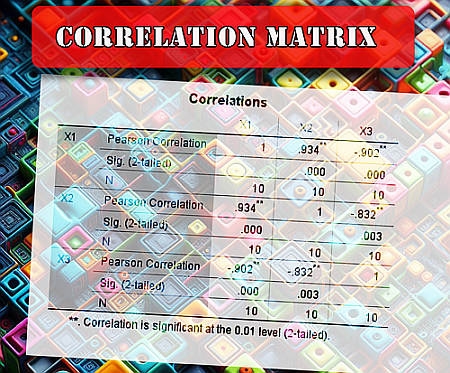
Ma c'è un'altra cosa da osservare: la correlazione tra \(X_1\) e \(X_2\) è la stessa correlazione tra \(X_2\) e \(X_1\), quindi la matrice di correlazione è simmetrico , quindi i valori sotto la diagonale rispecchiano ciò che hai sopra la diagonale.

Questo è il motivo per cui molto spesso si vede una matrice di correlazione con valori riportati solo sopra la diagonale (o sotto), perché sappiamo che la diagonale è 1, e sappiamo che i valori sotto la diagonale sono un riflesso speculare dei valori sopra la diagonale.