Algèbre Tutoriels

Recherche du graphique du journal

La manière de trouver le graphe log est commune à toutes les fonctions logarithmiques. C'est parce que toutes les fonctions logarithmiques ont essentiellement la même forme, au moins structurellement, cela ne dépend que de la base du logarithme.

Rappelons d'abord la fonction logarithmique de base \(a\), \(\log_a x\). Les bases les plus couramment utilisées sont pour \(a = 10\), auquel cas nous écrivons simplement \(\log x\), et le cas où \(a = e\), auquel cas nous écrivons \(\ln x\), et nous l'appelons le journal naturel.

Par exemple, le graphique de la fonction de log naturel, \(\ln x\) est illustré ci-dessous:

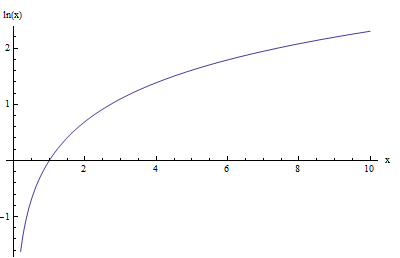
Voyons maintenant ce qui se passe lorsque nous représentons le graphique ensemble \(\log x\) et \(\ln x\) (c'est le log base 10 et le log naturel):

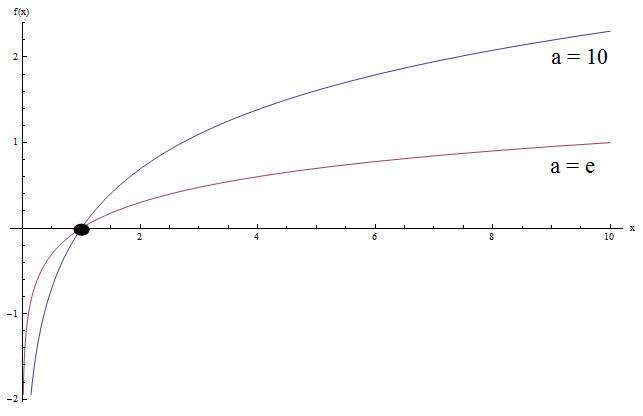
Voyez-vous des similitudes? Eh bien, il y en a.

Notez que les deux graphiques ont la même forme générale concave. De plus, les deux graphiques croisent l'axe des y à \(x = 1\) (ce qui n'est pas une surprise puisque \(\log_a 1 = 0\) pour toutes les bases, avec \(a > 0\)).

Une autre chose est que les deux graphes s'approchent de l'infini négatif lorsque \(x\) s'approche de 0, et de l'infini lorsque \(x\) s'approche de l'infini.

Et si nous essayons de représenter graphiquement des fonctions logarithmiques avec \(0 < a < 1\) ?. Consultez l'exemple ci-dessous:

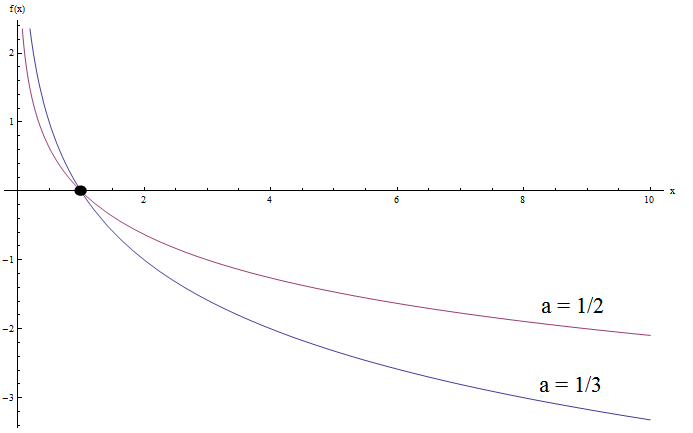
Fonctions de journal avec une base inférieure à 1

Voyez-vous des similitudes maintenant? Bien sûr.

Notez que les deux graphiques ont la même forme générale convexe. De plus, les deux graphiques croisent à nouveau l'axe des y à \(x = 1\), ce qui est attendu.

Mais maintenant, les deux graphiques se rapprochent de l'infini lorsque \(x\) s'approche de 0, et de l'infini négatif lorsque \(x\) s'approche de l'infini. C'est un peu le comportement opposé lorsque la base \(a\) est supérieure à 1.

Comment créer un graphique journal?

Sur la base de ce que nous avons trouvé dans les exemples précédents, nous pouvons ajouter quelques règles que vous pouvez utiliser lorsque vous souhaitez créer des graphiques de journal:

Supposons que vous vouliez représenter graphiquement la fonction \(y = \log_a x\), pour \(a > 0\). Puis:

Étape 1 : TOUJOURS, la fonction logarithmique croise l'axe des y à \(x = 1\).

Étape 2 : Si \(a > 1\), alors le graphique est croissant et concave. Aussi:

\[\lim_{x\to 0^+} \log_a x = -\infty, \,\, \lim_{x\to \infty} \log_a x = \infty\]

Étape 3 : Si \(0 < a < 1\), alors le graphe est décroissant et convexe. Aussi:

\[\lim_{x\to 0^+} \log_a x = \infty, \,\, \lim_{x\to \infty} \log_a x = -\infty\]

Facile, non ??

En savoir plus sur les graphiques log

Tout d'abord, savoir tracer une fonction est une compétence cruciale, étant donné que le graphe d'une fonction vous donne BEAUCOUP d'informations à ce sujet.

Dans les sections précédentes, nous avons appris comment la base d'un journal affecte le graphique. La chose intéressante est que la forme et le comportement du graphe logarithmique dépendent uniquement de savoir si \(a > 1\) et \(0 < a < 1\).

Un journal peut-il être égal à un nombre négatif?

Eh bien, nous devons préciser ce que nous entendons par là. Premièrement, la base de la fonction logarithmique ne peut pas être négative. De plus, l'argument d'une fonction logarithmique ne peut pas non plus être négatif.

MAIS, le logarithme d'un nombre peut absolument être négatif. Par exemple: \(\ln(1/e) = -1\).

Comment représenter graphiquement les fonctions de log inverse?

Eh bien, la première chose que vous devez savoir est que l'inverse d'une fonction log sera toujours une fonction exponentielle.

Ainsi, la représentation graphique de l'inverse d'une fonction log est aussi simple que de savoir quelle est l'exponentielle correspondante et de la représenter graphiquement.

Il existe également d'autres méthodes. Vous pouvez dessiner le graphe log original et dessiner un graphe symétrique à ce graphe log donné, par rapport au 45 ^o ligne droite \(y = x\).

Ou, utilisez le graphique d'origine et modifiez la valeur de \(x\) par la valeur de \(y\).

Ce tutoriel est orienté vers les propriétés graphiques de la fonction logarithmique. Pour le définition et règles de base du journal, vérifiez celle-ci .