Règles de journalisation
La fonction logarithmique est l'une des fonctions les plus importantes de Math, et les règles de journalisation sont simples et pratiques, ce qui facilite grandement l'utilisation des logarithmes.
Rappelons d'abord quelle est la signification de \(\log_b a\). Dans ce contexte, la valeur \(b\) est le base du logarithme, et \(a\) est le argument .
Nous disons que \(\log_b a = y\) lorsque \(b^y = a\). Cela signifie que \(\log_b a\) est le nombre désigné \(b\) (la base) doit être élevé pour obtenir \(a\) (l'argument).
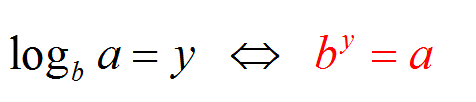
Par exemple, \(\log_{10} 25\) correspond au nombre auquel j'ai besoin d'élever 10 pour obtenir 25. Donc le logarithme que je recherche est le nombre \(y\) qui a la propriété \(10^y = 25\)
Maintenant, la question est de savoir comment calculer ce nombre \(y\) qui a la propriété \(10^y = 25\)? Eh bien, ce nombre est bien défini et la fonction logarithmique \(f(x) = \log_{10} x\) s'en charge. Cette fonction n'est pas une fonction élémentaire, et une série de Taylor (série infinie) est nécessaire pour la révision.
Ou, vous pouvez utiliser une calculatrice (ce qui est probablement plus facile, non?).
Les règles de journal: propriétés des logarithmes
Voici les principales règles de journalisation:
Règle 1 : \(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
Règle n ° 2 : \(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
Règle n ° 3 : \(\large \log_a (b^c) = c \cdot \log_a (b) \)
Règle n ° 4 : \(\large \log_a (a) = 1 \)
Règle n ° 5 : \(\large \log_a (1) = 0 \)
EXEMPLE 1
Simplifiez \(\log_2 8 + \log_2 4\) à l'aide des règles de journalisation:
RÉPONDRE:
En utilisant la règle n ° 1, nous constatons que:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]Donc, la première étape est une application simple de la règle n ° 1, mais comment pouvez-nous obtenir cela \(\log_2 32 = 5\)? C'est parce que \(2^5 = 32\), donc dans ce cas nous trouvons directement quel est le nombre dont vous avez besoin pour lever \(2\) afin d'obtenir \(32\).
La majorité des logarithmes vous aurez besoin d'une calculatrice pour les calculer. Ce ne sont que quelques-uns que vous pouvez calculer directement. Des trucs comme \(\log_{10} 100 = 2\), parce que vous savez facilement que \(10^2 = 100\).
Mais, pouvez-vous calculer \(\log_{10} 102\) directement? Pas vraiment, vous avez besoin d'une calculatrice pour cela.
EXEMPLE 2
Exprimez la somme et la soustraction des logarithmes: \( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \).
RÉPONDRE:
Tout d'abord, nous devons nous rappeler que prendre une racine cubique est le plus élevé à la puissance \(1/3\). En d'autres termes, \(\sqrt[3]{x}\) est identique à \(x^{1/3}\).
Donc, nous utilisons d'abord la règle n ° 3 pour amener la puissance devant le logarithme, puis nous utilisons les règles n ° 1 et n ° 2. Sur un:
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]ce qui était nécessaire: somme et soustractions de logarithmes simples.
Le changement de formule de base pour les logarithmes
L’ensemble des formules les plus utiles concernant les logarithmes est le changement de formule de base. Cette formule va comme ceci:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]Cette formule dit simplement que si vous voulez changer la base de \(b\) à \(c\), les résultats sont essentiellement les mêmes, mais vous devez diviser par le logarithme de la nouvelle base.
Maintenant, si vous êtes orienté artistique, vous pouvez profiter de la forme alternative du changement de formule de base exprimée ci-dessous:
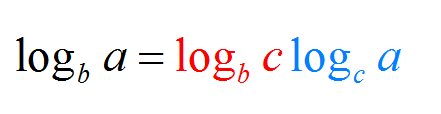
EXEMPLE 3
Exprimez le journal naturel \(\ln\) en termes de \(\log\) (base 10).
RÉPONDRE:
En utilisant le changement de formule de base, nous obtenons que:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]Donc, vous dites que \(\ln a\) est obtenu en divisant \(\log a\) par \(\log e\). Comme c'est pratique? Qui a dit que les maths étaient difficiles, hein?
En savoir plus sur les règles de journalisation
Les logarithmes sont vraiment importants en mathématiques. Historiquement, les logarithmes jouent un rôle très important en astronomie, comme moyen de prédire le mouvement de la lune et des planètes.
Les fonctions logarithmiques se trouvent au milieu de tout en Math, elles s’entremêlent avec les exponentiels, les exposants et à peu près tout. C'est pourquoi ils vous demandent d'apprendre les logarithmes par cœur, car ils sont importants.
De plus, ces règles de journalisation présentées ici jouent un rôle crucial pour faciliter la résolution d'équations logarithmiques .
Conventions de notation
Il y a quelques conventions de notation que vous devez connaître. En général, sur écrit \(\log_b a\), et sur dit "log base b de a". Lorsque la base est \(b = 10\), par convention, nous écrivons simplement \(\log a\). Ainsi, lorsque vous voyez un \(\log\) sans base, on suppose que la base est \(10\).
Il y a un autre cas notable. Pour \(\log_b a\), lorsque la base est \(b = e\) (la constante d'Euler), alors nous écrivons \(\ln a\) au lieu de \(\log_e a\). Ainsi, lorsque \(\ln\) est utilisé à la place de \(\log\), c'est parce que la base du logarithme est \(e\).
Observez que \(\ln a\) est généralement appelé bûche naturelle . Et oui, les journaux naturels ont les mêmes règles que le journal général.
Si vous avez une fonction logarithmique que vous souhaitez éditer graphiquement, vous pouvez essayer notre Créateur de graphes de fonctions logarithmiques , qui vous fournira un graphique parfaitement présenté.
