Formule d'élasticité de l'arc pour une table

La formule d'arc-élasticité de la demande vous permet d'estimer l'élasticité aux points donnés dans un tableau de planification de la demande, sans avoir de formule explicite pour la fonction de demande.

Ce que vous devez fournir est un tableau avec une colonne pour le prix et une colonne pour la quantité demandée. Une fois que cela est tapé ou collé dans la feuille de calcul fournie, vous cliquerez sur « Calculer » pour obtenir les élasticités d'arc correspondantes calculées pour vous.

Notez que ceci n'est qu'une approximation : la situation idéale est de calculer les élasticités en utilisant la fonction de demande , en utilisant des dérivés.

Étapes pour utiliser l'arc-elasticité pour une table

La formule d'élasticité de l'arc est :

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

et ceci peut être appliqué à des points consécutifs dans un tableau de planification de la demande. Vous suivrez ces étapes :

• Étape 1 : Indiquez correctement vos valeurs pour le prix (P) et la quantité demandée (Q)
• Étape 2 : Vous pouvez créer des colonnes pour Q2 - Q1, P2 - P1, Q1 + Q2 et P1 + P2 si vous souhaitez rendre les calculs plus clairs, ou vous pouvez calculer la formule directement
• Étape 3 : Il y aura un point sauté dans le tableau, puisque l'arc-élasticité prend un point sur le tableau et le point qui suit immédiatement dans le tableau

L’utilisation de cette approximation d’élasticité d’arc vous fournira une excellente image de la sensibilité aux variations de prix pour le bien spécifique analysé, même s’il ne s’agit que d’une approximation.

Plus nous avons de points de demande, meilleure sera l’approximation, surtout si ces points de prix sont proches les uns des autres.

Que mesure l'élasticité de l'arc ?

L'élasticité de l'arc vise à fournir une approximation de l'élasticité réelle à un point donné. L'élasticité réelle à partir de la courbe de demande est calculée par :

\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]

On pourrait arguer que l'élasticité de l'arc n'est qu'une approximation, alors pourquoi a-t-elle une quelconque valeur ? La réponse à cette question est que pour l'analyse de l'élasticité, et pour l'analyse de la sensibilité en économie en général, nous nous intéressons davantage aux plages de valeurs qu'à des points très précis.

En effet, à des fins microéconomiques, il est utile de savoir si nous sommes dans une zone inélastique ou non, plutôt que la valeur très spécifique de l'élasticité

Ce n’est pas que la valeur spécifique n’est pas importante, car c’est en effet une bonne chose de l’avoir, mais les élasticités d’arc sont souvent une bonne approximation, et elles nous donneront des représentations très précises du type de plage d’élasticité à laquelle nous sommes confrontés.

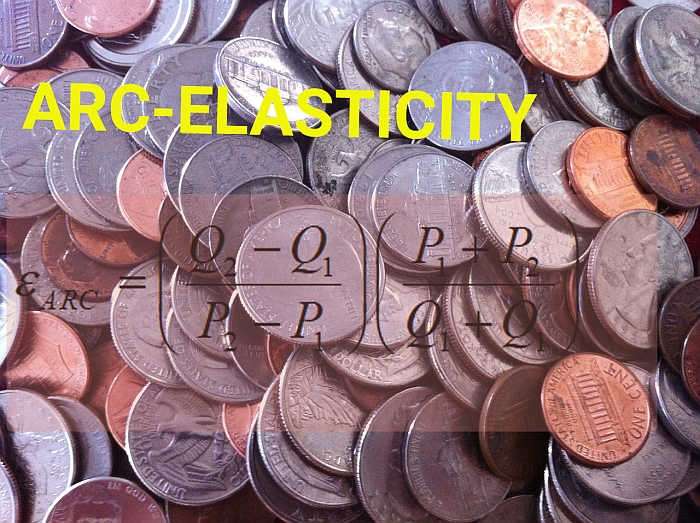
Exemple

Considérez le tableau de demande suivant avec des informations sur le prix et la quantité demandée

Fournissez l’approximation de l’élasticité de l’arc pour les points de données dans ce tableau.

P	Q
1	200
1.5	190
2	170
2.5	155
3	130
3.5	110
4	90
4.5	60

Solution : Afin d'estimer l'élasticité-prix de la demande à partir de ces données, nous devons utiliser la formule d'élasticité d'arc suivante

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

En appliquant la formule ci-dessus à toutes les paires de points de données consécutifs, nous trouvons les arc-élasticités suivantes :

P	Q	Élasticité De L'Arc
1	200	-
1.5	190	\(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\)
2	170	\(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\)
2.5	155	\(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\)
3	130	\(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\)
3.5	110	\(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\)
4	90	\(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\)
4.5	60	\(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\)

Interpretation

Le tableau ci-dessous montre l'élasticité-prix approximative de la demande pour chacun des niveaux de prix fournis. Ces valeurs peuvent être utilisées approximativement pour déterminer les plages élastiques et inélastiques du barème de demande fourni.

Autres calculatrices économiques

Si vous travaillez en économétrie, ceci Calculatrice de régression sera probablement utile, notamment parce qu'il montre toutes les étapes du processus de calcul des coefficients de régression .

Vous pouvez également utiliser un équation log-log pour estimer un courbe de demande à élasticité constante .