Règles des exposants
Les opérations avec des exposants sont parmi les opérations les plus courantes que vous effectuerez partout en mathématiques, et il est essentiel que vous ayez une base appropriée à leur sujet.
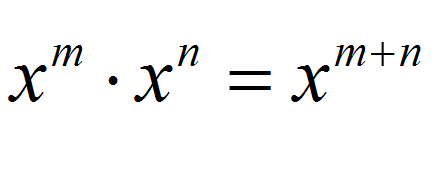
Sans plus tarder, énumérons les propriétés de base des exposants. L'utilisation efficace de ces propriétés est de la plus haute importance. Les règles sont:
Règle 1: \(\large \displaystyle x^0 = 1\), pour \(x = \not 0\)
Règle 2: \(\large\displaystyle x^1 = x\)
Règle 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Règle 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Règle 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Règle 6: \(\large\displaystyle (x \cdot y)^m = x^m \cdot y^m\)
Expliquons un peu ces règles dans les mots .
Règle 1
dit que tout ce qui est élevé à la puissance zéro est égal à 1. Eh bien, sauf pour 0, parce que par convention (et il y a une bonne raison à cela) \(0^0 = 0\).
Maintenant,
Règle 2
signifie que prendre n'importe quel nombre et l'élever à la puissance 1 donne le même nombre d'origine. En d'autres termes, élever un nombre à la puissance 1 n'affecte pas le nombre.
Règle 3
c'est dire que lorsque je multiplie des puissances avec la même base, le résultat est une puissance qui a la même base, élevée à une puissance qui correspond à la somme des exposants des puissances que je multiplie.
Règle 4
dit que prendre la puissance d'une puissance équivaut à prendre une puissance avec les exposants multipliés comme exposant.
Règle 5
c'est dire que lorsque je divise des puissances avec la même base, le résultat est une puissance qui a la même base, élevée à une puissance qui correspond à la soustraction des exposants des puissances que je multiplie.
Règle 6
c'est dire que quand j'ai un pouvoir affectant une multiplication, alors c'est la même chose que de multiplier chacun des termes élevés à ce pouvoir.
EXEMPLE 1
Simplifiez l'expression suivante
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2}\]RÉPONDRE:
En utilisant la règle 5 pour la division des pouvoirs avec la même base:
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2} = \frac{x^{3}y^{3}}{x^{1/2} y^2} \] \[\large \displaystyle = \frac{x^3}{x^{1/2}} \cdot \frac{y^3}{y^2} = \displaystyle x^{3-1/2} \cdot y^{3-2}\] \[\large \displaystyle = \displaystyle x^{5/2} \cdot y^{1} = x^{5/2} y\]Dois-je m'inquiéter des exposants négatifs?
Pas vraiment. Tout d'abord, les 5 règles pour les exposants énoncées ci-dessus ne font aucune déclaration spécifique indiquant que les exposants doivent être non négatifs. En fait, les règles fonctionnent quand même des exposants sont négatifs.
En effet, pour exposants négatifs , il y aura deux règles qui vous permettront de les transformer en exposants positifs:
\[\large\displaystyle \frac{1}{x^n} = x^{-n}\]
Cette expression ci-dessus nous montre que nous pouvons convertir une puissance avec un exposant négatif qui est dans le numérateur en une puissance dans le dénominateur avec l'exposant positif correspondant.
Cette expression ci-dessus nous montre que nous pouvons convertir une puissance avec un exposant négatif qui est dans le dénominateur en une puissance dans le numérateur avec l'exposant positif correspondant.
EXEMPLE 2
Simplifiez l'expression suivante en ne laissant aucun exposant négatif:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}}\]RÉPONDRE:
Transformer les exposants négatifs en exposants positifs et appliquer les 5 règles d'exposant:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}} = \frac{x^{4} x^{1/2} y^{-2}}{x^{-3/2} y^{1/2}} \] \[\large \displaystyle = \frac{x^{4} x^{1/2} x^{3/2}}{y^{1/2} y^{2}} = \frac{x^{4+1/2+3/2}}{y^{2+1/2}} \] \[\large \displaystyle = \frac{x^{6}}{y^{5/2}} \]ce qui conclut la simplification.
Ces règles exposantes sont-elles quelque peu liées aux règles des logarithmes?
Absolument! Vérifiez règles logarithmiques et vous découvrirez qu'ils sont structurellement très similaires, et c'est parce que les logarithmes et les puissances sont des opérations inverses les uns par rapport aux autres.
Juste comme un petit échantillon, faisons une preuve rapide. Supposons que \(a = x^m\) et \(b = x^n\). Ensuite, par définition, \(m = \log_x a\) et \(n = \log_x b\). Donc, par les règles d'exposant, \(a\cdot b = x^m \cdot x^n = x^{m+n}\). Par conséquent, par définition, \(m + n = \log_x (a \cdot b)\). Mais \(m = \log_x a\) et \(n = \log_x b\), donc \(\log_x a + \log_x b = \log_x (a \cdot b)\).
En savoir plus sur la règle des exposants
Une chose sur laquelle nous devons mettre l'accent est sur le fait que les règles pour les exposants n'exigent pas que les exposants soient positifs. Les exposants n'ont pas besoin d'être des nombres entiers. Les règles sont valables pour les vrais exposants.
• N'oubliez pas que si vous avez affaire à un exposant négatif dans le numérateur, vous pouvez le transformer en le passant au dénominateur à exposant positif.
• De plus, si vous avez affaire à un exposant négatif dans le dénominateur, vous pouvez le transformer en le passant au numérateur avec un exposant positif.
Les règles des exposants ont tellement d'applications, y compris fournir une base de base pour obtenir le règles de simplification des radicaux , qui viennent comme corollaire des racines des exposants.
En termes graphiques, vous pouvez explorer cette règle en représentation graphique de différentes fonctions exponentielles et voir leurs propriétés spécifiques.