Opérations avec des exposants négatifs
Les opérations avec exposants sont parmi les opérations les plus fondamentales de l'algèbre, et parmi elles, celles qui impliquent des exposants négatifs sont celles qui apportent le plus de complications aux étudiants.
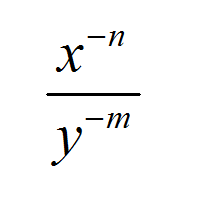
Tout d'abord, rappelons les propriétés de base des exposants. L'utilisation de ces propriétés est omniprésente dans la plupart des domaines des mathématiques. Les règles sont:
Règle 1: \(\large \displaystyle x^0 = 1\), pour \(x = \not 0\)
Règle 2: \(\large\displaystyle x^1 = x\)
Règle 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Règle 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Règle 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Par exemple, lorsque vous avez une expression comme \(3^5 \cdot 3^7\), nous savons que nous utilisons la règle de multiplication (règle 3) pour obtenir:
\[\large 3^5 \cdot 3^7 = 3^{5+7} = 3^{12}\]Les règles des exposants: qu'arrive-t-il aux exposants négatifs?
Même si vous ne vous en êtes pas rendu compte, les règles ci-dessus ne disent pas que les exposants doivent être positifs. En effet, ils pourraient être négatifs et les règles s'appliqueront également.
Maintenant, à partir des règles 1 et 5, nous pouvons déduire la relation entre les exposants positifs et négatifs. Donc, pour la règle 5, supposons que \(m = 0\) et \(n\) sont positifs. Ensuite, nous obtenons
\[\large\displaystyle \frac{1}{x^n} = \frac{x^0}{x^n} = x^{0-n} = x^{-n}\]L'expression ci-dessus nous donne une relation simple entre les exposants positifs et négatifs:
\[\large\displaystyle \boxed{\frac{1}{x^n} = x^{-n}}\]
Cette expression ci-dessus nous dit que nous pouvons passer une puissance avec un exposant négatif dans le numérateur au dénominateur avec l'exposant positif correspondant. C'est une `` règle '' d'exposants négatifs
La beauté de la formule ci-dessus est que nous pouvons multiplier les termes des deux côtés de l'égalité, et nous pouvons écrire l'expression ci-dessus sous une forme légèrement différente:
\[\large\displaystyle \boxed{\frac{1}{x^{-n}} = x^{n}}\]
Cette dernière expression est généralement très utile, car elle nous dit que nous pouvons amener une puissance avec exposant négatif dans le dénominateur au numérateur mais avec l'exposant positif correspondant. Cela peut être considéré comme une autre "règle" pour les exposants négatifs.
EXEMPLE 1
Simplifiez l'expression suivante et laissez sans exposants négatifs:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2}\]RÉPONDRE:
En utilisant la règle des exposants négatifs, nous commutons les exposants positifs / négatifs entre numérateur / dénominateur:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2} = \frac{x^{3}\sqrt{x} x^{1/2}}{ y^2 y^{3}}\] \[\large = \frac{x^{3} x^{1/2} x^{1/2}}{ y^2 y^3} = \frac{x^{3+1/2+1/2}}{ y^{2+3}} \] \[\large = \frac{x^{4}}{ y^{5}} \]et nous terminons la simplification, car il n'y a plus rien à simplifier.
En savoir plus sur les exposants négatifs
L'un des plus grands enseignements de ce tutoriel sur les exposants négatifs est que nous avons des règles pour transformer ces exposants négatifs en exposants positifs. Comment fait-on cela?
• Si nous avons un exposant négatif dans le numérateur (donc vous multipliez par un exposant négatif), nous pouvons le passer au dénominateur avec un exposant positif.
• Si nous avons un exposant négatif dans le dénominateur (donc vous divisez par un exposant négatif), nous pouvons le passer au numérateur avec un exposant positif.
Utiliser des exposants négatifs n'est qu'une petite partie du sujet de la gestion règles des exposants , qui vous donnent un aperçu clair de la raison pour laquelle le cas avec des exposants négatifs fonctionne comme il le fait.