Comment trouver la plage
Apprendre à trouver la plage d'une fonction peut s'avérer très important en Algèbre et Calcul, car cela vous donne la possibilité d'évaluer quelles valeurs sont atteintes par une fonction. Ou en d'autres termes, il permet de retrouver l'ensemble de toutes les images via la fonction
La tâche de trouver quels points peuvent être atteints par une fonction est très utile. Par exemple, vous pouvez avoir une fonction de production \(q(x)\), qui vous donne la quantité de sortie obtenue pour \(x\) unités d'entrée.
Nous aimerions savoir combien d'unités d'entrée sont nécessaires pour produire des unités de sortie \(b\). Donc, en d'autres termes, nous devons trouver \(x\) pour que \(q(x) = b\), qui est une autre façon de demander si \(b\) est dans la plage de la fonction \(q(x)\).
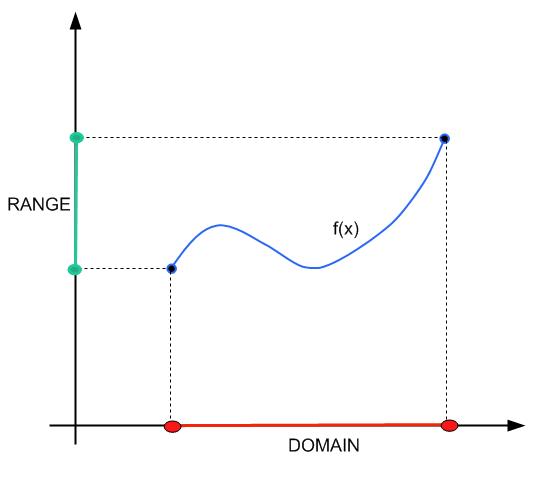
Dans ce tutoriel, nous nous concentrerons davantage sur les mécanismes de recherche de la gamme. Pour une approche plus conceptuelle du domaine et de la plage, vous pouvez voir ce tutoriel .
La manière algébrique de trouver la plage d'une fonction
Idem que lorsque nous avons appris à calculer le domaine, il n'y a pas une seule recette pour trouver la plage, cela dépend vraiment de la structure de la fonction \(f(x)\).
Pourtant, il existe une technique algébrique qui sera toujours utilisée. C'est LA façon dont vous trouvez la gamme. Faites attention:
Disons que nous devons obtenir la plage d'une fonction donnée \(f(x)\). Ensuite, nous considérerons un nombre réel générique \(y\) et nous essaierons de résoudre pour \(x\) l'équation suivante:
\[f(x) = y\]Nous devons déterminer pour quelles valeurs de \(y\) l'équation ci-dessus peut être résolue pour \(x\). C'est ça. Bien sûr, cela peut être difficile à faire, selon la structure de la fonction \(f(x)\), mais c'est ce que vous devez faire.
C'est donc la manière algébrique, la manière de trouver la plage d'une fonction sans graphisme.
EXEMPLE 1
Trouvez la plage de la fonction \(\displaystyle f(x) = \frac{x+1}{x-3}\):
RÉPONDRE:
Nous procédons de la manière algébrique: Soit \(y\) un nombre et nous résoudrons pour \(x\) dans l'équation suivante: \(f(x) = y\). La valeur \(y\) est dans la plage si \(f(x) = y\) peut être résolue pour \(x\).
Dans ce cas, nous avons:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]Par conséquent, quand \(x\) sera-t-il bien défini? Presque pour tous les \(y\), sauf quand \(y = 1\), car dans ce cas nous avons une division par \(0\). Par conséquent, la plage de \(f\) dans ce cas est la ligne réelle entière, à l'exception de 1.
Si nous utilisons la notation d'intervalle, nous pouvons écrire \(Range(f) = (-\infty, 1) \cup (1, +\infty)\).
EXEMPLE 2
Trouvez la plage de la fonction \(f(x) = x^2 - 4x + 3\):
RÉPONDRE:
Encore une fois, nous procédons en utilisant la méthode algébrique, donc vous connaissez l'exercice: Soit \(y\) un nombre et nous résoudrons pour \(x\) dans l'équation suivante: \(f(x) = y\). La valeur \(y\) est dans la plage si \(f(x) = y\) peut être résolue pour \(x\).
Dans ce cas, nous avons:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]Maintenant, vu cette expression finale, quand \(x\) sera-t-il bien défini? Nous devons avoir que l'argument de la racine carrée doit être non négatif, nous avons donc besoin de:
\[1+y \ge 0\]ce qui signifie que \(y \ge -1\). Si nous utilisons la notation d'intervalle, nous pouvons écrire \(Range(f) = [-1, +\infty)\).
Dans cet exemple, nous aurions pu le résoudre en utilisant le fait que \(f(x) = x^2 - 4x + 3\) est une fonction quadratique et que son graphe est une parabole qui s'ouvre vers le haut.
Le point minimum de cette parabole est atteint au sommet. La coordonnée x du sommet est:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]Maintenant, la coordonnée y du sommet est simplement trouvée en branchant la valeur \(x_V = 2\) dans la fonction quadratique:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]Puisque la valeur minimale atteinte par la parabole est \(-1\), nous concluons que l'intervalle est \([-1, +\infty)\), ce qui est la même conclusion que celle trouvée algébriquement.
Le graphique de la fonction \(f(x) = x^2 - 4x + 3\) le rend encore plus clair:
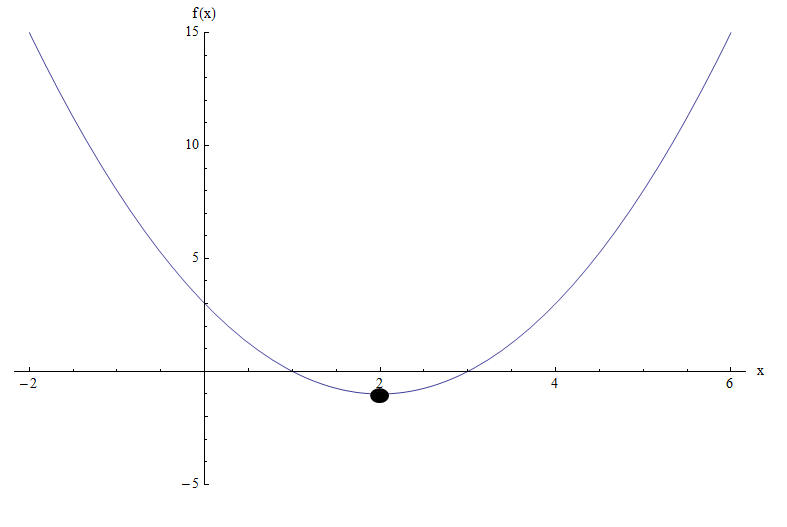
Nous pouvons voir que, sur la base du graphique, le minimum est atteint à \(x = 2\), qui est exactement ce qui a été trouvé à la coordonnée x du sommet.
Le risque d'utiliser le graphique pour trouver la plage est que vous pourriez mal interpréter les points critiques du graphique et donner une évaluation inexacte de l'endroit où la fonction atteint son maximum ou son minimum.
Autres stratégies pour trouver la portée d'une fonction
Comme nous l'avons vu dans l'exemple précédent, nous pouvons parfois trouver la plage d'une fonction en regardant simplement son graphique.
Par exemple, supposons que vous souhaitiez trouver la plage de la fonction \(f(x) = x + 3\). Le graphique est présenté ci-dessous:
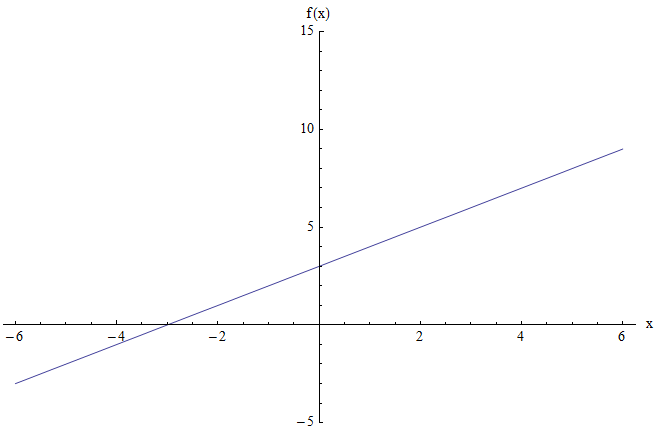
Le graphique ci-dessus ne montre aucun point minimum ou maximum. De plus, lorsque \(x\) est grand et positif, la valeur de la fonction est également grande et positive. Et de manière analogue, lorsque \(x\) est très négatif, la valeur de la fonction est également très négative.
L'intuition est que la fonction peut prendre des valeurs aussi négatives et positives que nous le voulons, en sélectionnant des valeurs \(x\) suffisamment grandes (positives ou négatives). Et puis, la conclusion est que la plage est la ligne réelle entière, qui est \((-\infty, +\infty)\) en utilisant la notation d'intervalle.
Une telle analyse est correcte en termes de résultat, mais elle est fragile en termes de raisonnement. La "méthode graphique" pour trouver la gamme a ce problème: elle est séduisante d'un point de vue intuitif, mais elle est plutôt mince en termes de contenu.
Normalement, si possible, nous devrions préférer la méthode analytique / algébrique. Dans l'exemple, nous devons résoudre pour \(x\):
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]Alors, y a-t-il une restriction sur \(y\) pour que \(x\) soit bien défini? Pas du tout, donc, il n'y a aucune restriction sur \(y\) et la conclusion est que la plage est la ligne réelle entière.
Vous pouvez consulter cet article que vous souhaitez savoir trouver le domaine d'une fonction au lieu.
Il existe de nombreuses bonnes raisons algébriques pour trouver la plage, l'une d'elles est qu'elle fait partie des processus pour trouver l'inverse d'une fonction .
