Comment trouver un domaine
Apprendre à trouver le domaine d'une fonction est une compétence cruciale en Algèbre, car elle vous donne la capacité d'évaluer où une fonction est correctement définie. Ou en d'autres termes, la région où il est valide de faire fonctionner la fonction
La tâche de trouver où il est valide d'exploiter une fonction est utile. Par exemple, considérons la fonction \(f(x) = \sqrt x\). Nous savons que la fonction opère des valeurs telles que \(x \ge 0\). Nous ne pouvons pas travailler avec des nombres négatifs, car nous obtiendrions quelque chose comme \(f(-1) = \sqrt{-1}\), qui n'est pas bien défini (au moins comme un nombre réel)
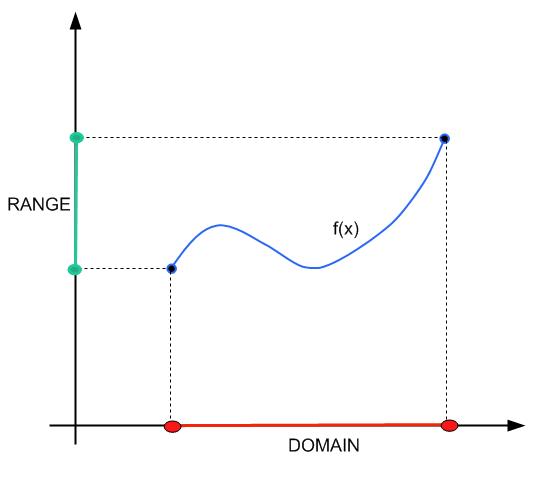
Vous pouvez consulter notre tutoriel précédent dans lequel nous avons parlé en profondeur de la domaine et plage . Ce tutoriel sera orienté vers la partie opérationnelle de la recherche du domaine.
Pourquoi avons-nous besoin de trouver le domaine?
La raison pour laquelle nous devons trouver le domaine d'une fonction est que chaque fonction a un ensemble spécifique de valeurs où elle est définie. Toutes les fonctions ne sont pas définies partout dans la ligne réelle.
Le domaine la région dans la ligne réelle où il se trouve valide pour travailler avec la fonction \(f(x)\), en termes de valeurs que \(x\) peut prendre.
Que devons-nous faire pour trouver le domaine?
Vraiment, il n'y a pas une astuce qui convient à toutes les tailles. Chaque fonction est différente et différentes stratégies doivent être utilisées pour trouver le domaine, en fonction de la fonction.
Vous devez TOUJOURS prendre en compte deux techniques:
Technique 1
: Assurez-vous qu'il existe des divisions par zéro.
De plus, les points qui conduisent à une division par zéro doivent être exclus du domaine.
Technique 2
: Assurez-vous qu'il existe des divisions racines carrées avec des arguments négatifs (comme \(\sqrt{-1}\)).
De plus, les points qui conduisent à une racine carrée d'un nombre négatif doivent être exclus du domaine.
En fin de compte, en utilisant ces deux techniques, vous devriez être en mesure d'éliminer les points qui ne sont pas dans le domaine. Les autres points de la ligne réelle font simplement partie du domaine.
Ainsi, ces deux techniques résolvent le problème de savoir trouver le domaine d'une fonction algébriquement. Une autre façon de le faire est de regarder le graphique, s'il est disponible.
EXEMPLE 1
Trouvez le domaine de la fonction \(f(x) = \sqrt{x+4}+3\)
RÉPONDRE:
La première chose que nous devons faire, et c'est là que réside notre succès dans la recherche du domaine, est de déterminer où nous pourrions potentiellement trouver des opérations invalides, telles que des divisions par zéro ou des racines carrées négatives.
Pour la fonction \(f(x) = \sqrt{x+4}+3\), il n'y a pas de division potentielle par zéro, mais il y a une racine carrée. Pour avoir un argument valide, l'argument à l'intérieur de la racine carrée doit être non négatif.
Par conséquent, pour que \(x\) soit dans le domaine de la fonction, nous devons avoir \(x\ge 0\). Cela implique que le domaine de \(f\) est \(\{x: x\ge 0\}\), ou \([0, +\infty)\) si nous utilisons la notation d'intervalle.
Est-ce toujours aussi simple? Pas vraiment, cela peut devenir aussi difficile que possible, selon la complexité de la fonction \(f(x)\).
Normalement, cependant, les exemples que vous voyez dans vos tests et vos devoirs sont plutôt simples. Frappons un cran plus haut en termes de difficulté.
EXEMPLE 2
Recherchez maintenant le domaine de la fonction \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\)
RÉPONDRE:
Cette fonction est un peu plus complexe et nécessite un traitement plus soigné. Dans ce cas, nous devons nous soucier des divisions possibles par zéro et par des racines carrées négatives.
Premièrement, il pourrait y avoir une division potentielle par zéro, lorsque \(x = 3\), ce qui indique que \(x = 3\) doit être exclu du domaine.
Maintenant, nous devons nous occuper d'une racine carrée négative potentielle. Nous devons évaluer le signe de \(\displaystyle \frac{x+4}{x-3}\). De plus, nous avons besoin que ce soit non négatif, nous devons donc résoudre:
\[\displaystyle \frac{x+4}{x-3} \ge 0\]Pour qu'une division ne soit pas négative, il faut que le numérateur et le dénominateur soient positifs, ou que le numérateur et le dénominateur soient négatifs.
En d'autres termes, il nous faut à la fois \(x+4 \ge 0\) et \(x-3 > 0\), ou les deux \(x+4 \le 0\) et \(x-3 < 0\).
C'est la même chose que \(x \ge -4\) et \(x > 3\), ou les deux \(x \le -4\) et \(x < 3\).
Et cela peut être écrit comme \(x > 3\), ou les deux \(x \le -4\), ce qui correspond à l'intervalle \( (-\infty, -4] \cup (3, +\infty)\).
La conclusion est que le domaine de la fonction \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) est:
\[ dom(f) = (-\infty, -4] \cup (3, +\infty)\]Comme vous pouvez le voir, le niveau de difficulté a un peu augmenté et vous pouvez en fait l'augmenter autant que vous le souhaitez.
Comment trouver le domaine d'une fonction rationnelle
Tout d'abord, rappelons qu'une fonction rationnelle est le quotient de deux polynômes, de la forme:
\[f(x) = \frac{p(x)}{q(x)} = \frac{a_0 + a_1 x + ...+ a_m x^m}{b_0 + b_1 x + ...+ b_n x^n}\]Comment trouvez-vous le domaine de la fonction rationnelle ci-dessus? Nous devons suivre notre règle: recherchez les divisions potentielles par zéro et des racines carrées négatives.
Dans ce cas, il n'y a pas de racines carrées négatives potentielles, mais il pourrait y avoir des divisions par zéro, partout où le polynôme qui est dans le dénominateur est zéro.
La conclusion est très simple: le domaine d'une fonction rationnelle est la ligne réelle entière SAUF pour les points où le polynôme du dénominateur est nul.
EXEMPLE 3
Trouvez le domaine de
\[f(x) = \frac{x^2 + x + 1}{x^3 - 6x^2 + 11x - 6}\]RÉPONDRE:
Tout d'abord, nous devons comprendre qu'il s'agit d'une fonction rationnelle, car vous avez respectivement deux polynômes \(p(x) = x^2 + x + 1\) et \(q(x) = x^3 - 6x^2 + 11x - 6\) dans le numérateur et le dénominateur.
Alors, la première étape consiste à trouver les zéros du polynôme dans le dénominateur, nous devons donc résoudre: \[ x^3 - 6x^2 + 11x - 6 = 0\]
Cette équation est en quelque sorte difficile à résoudre, donc je vais vous donner cela en fait \(x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3)\), alors nous devons résoudre:
\[ x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3) = 0\]ce qui signifie que les racines du polynôme dans le dénominateur sont \(x_1 = 1, x_2 = 2, x_3 = 3\). La conclusion est que le domaine de la fonction est la ligne réelle entière, à l'exception des points 1, 2 et 3. En utilisant la notation d'intervalle, le domaine est \((-\infty, +\infty) \backslash \{1,2,3\}\).
Autres stratégies pour trouver le domaine d'une fonction
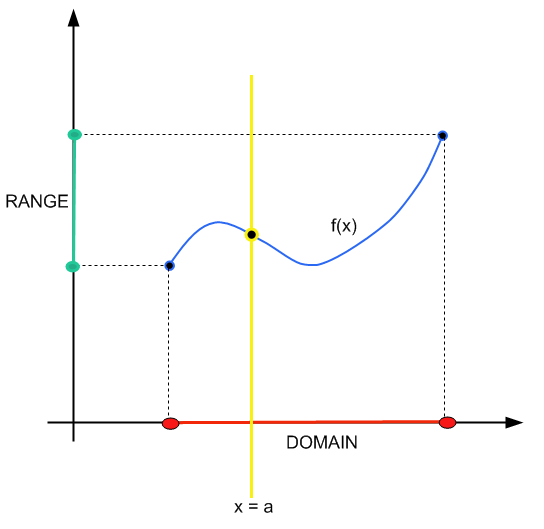
L'alternative de trouver le domaine d'une fonction en regardant les divisions potentielles par des racines carrées nulles ou négatives, ce qui est la manière analytique, est de regarder le graphique.
La méthode est simple: vous construisez une ligne verticale \(x = a\). Si cette ligne verticale croise le graphique de la fonction en un et un seul point, alors \(x = a\) appartient au domaine.
Court et doux.
Enfin, comment trouver le domaine d'une fonction avec une racine carrée
C'est le cœur de l'une des techniques dont nous avons parlé, qui consiste à trouver des racines carrées négatives potentielles. Donc, lorsque vous avez une fonction avec une ou plusieurs racines carrées, vous savez qu'il est très probable que vous ayez une racine négative potentielle, et vous devez la détecter.
Ce n'est pas toujours le cas, cependant. Pensez à la fonction \(f(x) = \sqrt{x^2}\). Cette fonction a une racine carrée, mais l'argument à l'intérieur est \(x^2\), qui ne peut pas être négatif, nous avons donc le cas d'une fonction avec une racine carrée qui n'a pas de racines carrées négatives.