Comment trouver l'inverse d'une fonction
De nombreuses applications en algèbre et calcul dépendent de savoir comment trouver l'inverse d'une fonction, et c'est le sujet de ce didacticiel.
Tout d'abord, vous devez réaliser qu'avant de trouver l'inverse d'une fonction, vous devez vous assurer que cet inverse existe.
L'avantage de la méthode de recherche de l'inverse que nous utiliserons est que nous allons trouver l'inverse et savoir s'il existe ou non en même temps.
Prêt?? Bouclez-vous alors.
Comment savoir si une fonction a un inverse?
Techniquement, une fonction a un inverse lorsqu'elle est un-à-un (injective) et surjective.
La condition cruciale est cependant qu'elle doit être un-à-un, car une fonction peut être rendue surjective en limitant sa portée à sa propre image.
Comment savoir quand une fonction est individuelle?
Eh bien, il y a au moins deux façons. L'une est la manière algébrique, et l'autre est la manière graphique (je parie que je sais laquelle vous préférez, hein?)
Voie algébrique
Pour la manière algébrique, pour qu'une fonction \(f\) soit un-à-un, nous devons prouver que chaque fois que \(f(x) = f(y)\), nous devons avoir cela \(x = y\).
En d'autres termes, nous devons prouver que
\[f(x) = f(y) \,\,\Rightarrow \,\, x = y\]
Manière graphique
Pour la manière graphique, nous devons utiliser le test de ligne horizontale : Pour toute ligne horizontale que nous dessinons, le graphique de la fonction traverse au plus une fois cette ligne horizontale.
Graphiquement:
Il réussit le test de la ligne horizontale
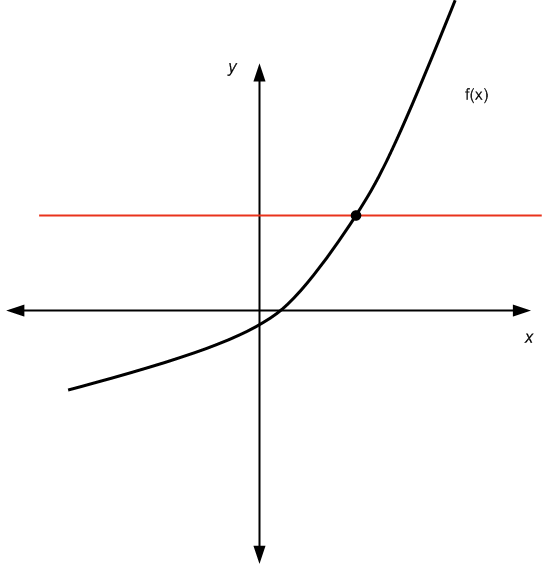
Il ne passe pas le test de la ligne horizontale
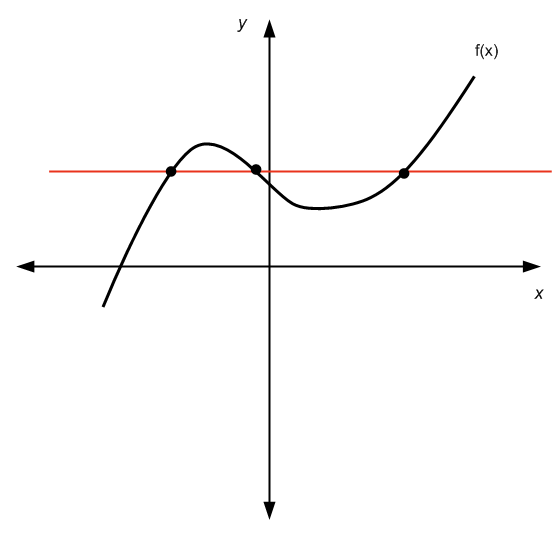
Trouver l'inverse
Trouver l'inverse d'une fonction donnée \(f(x)\) vous oblige à résoudre une équation.
En effet, vous avez l'équation \(f(x) = y\), vous prenez \(y\) comme un nombre donné, et vous devez le résoudre pour \(x\), et vous devez vous assurer que la solution est UNIQUE.
C'est tout. Facile, non ??
Passons maintenant aux étapes pratiques:
Étape 1:
Pour un \(y\) donné, définissez l'équation:
et résolvez-le pour \(x\).
Étape 2:
Assurez-vous de faire attention pour voir pour quel \(y\), il existe en fait une solution unique.
Étape 3:
Une fois que vous avez résolu \(x\) en termes de \(y\), cette expression qui dépend de \(y\) sera votre \(f^{-1}(y)\).
Étape 4:
Changez le nom de la variable de \(y\) à \(x\) et vous avez votre fonction inverse \(f^{-1}(x)\).
EXEMPLE 1
Trouvez l'inverse de la fonction \(f(x) = \sqrt x\)
RÉPONDRE:
Donc, nous prenons \(y\) comme donné et nous devons résoudre \(f(x) = y\), ce qui dans ce cas correspond à la résolution
\[\sqrt x = y\]Notez que la racine carrée est toujours non négative, donc pour avoir une solution, nous avons besoin de \(y\ge 0\).
En appliquant le carré des deux côtés, nous obtenons cela
\[\Rightarrow \,\, (\sqrt x)^2 = y^2\] \[\Rightarrow \,\, x = y^2\]Donc, \(f^{-1}(y) = y^2\), et en changeant le nom de la variable, nous avons la fonction inverse est
\[f^{-1}(x) = x^2\]pour \(x\ge 0\).
EXEMPLE 2
Trouvez l'inverse de la fonction \(f(x) = \displaystyle \frac{x}{x+1}\), pour \(x > -1\)
RÉPONDRE:
Encore une fois, nous prenons \(y\) comme donné, et maintenant nous devons résoudre pour \(x\) l'équation \(f(x) = y\). Nous avons donc
\[\displaystyle \frac{x}{x+1} = y\] \[\Rightarrow \,\, x = y(x+1)\] \[\Rightarrow \,\, x = yx + y\] \[\Rightarrow \,\, x - yx = y\] \[\Rightarrow \,\, x(1 - y) = y\] \[\Rightarrow \displaystyle \,\, x = \frac{y}{1-y}\]Donc, \(f^{-1}(y) = \displaystyle \frac{y}{1-y}\), et en changeant le nom de la variable, nous avons la fonction inverse est
\[f^{-1}(x) = \displaystyle \frac{x}{1-x}\]En savoir plus sur la recherche de l'inverse d'une fonction
L'une des propriétés cruciales de la fonction inverse \(f^{-1}(x)\) est que \(f(f^{-1}(x)) = x\).
Pensez à ce que dit cette chose. Quelque chose comme: "La fonction évaluée à l'inverse vous donne l'identité".
Ou en d'autres termes, évaluer l'inverse via la fonction revient à ne rien faire à l'argument.
Ou comme certains aiment le dire: la fonction peut annuler l'inverse d'une certaine manière.
Vous choisissez votre version.
Comment trouver l'inverse d'une fonction quadratique? Peut tu?
En fait, la réponse est: cela dépend. En effet, si nous considérons une fonction quadratique sur toute la ligne réelle , alors ce n'est pas 1 pour 1, car il ne passe pas le test de la ligne horizontale, comme vous pouvez le voir dans le tableau ci-dessous:
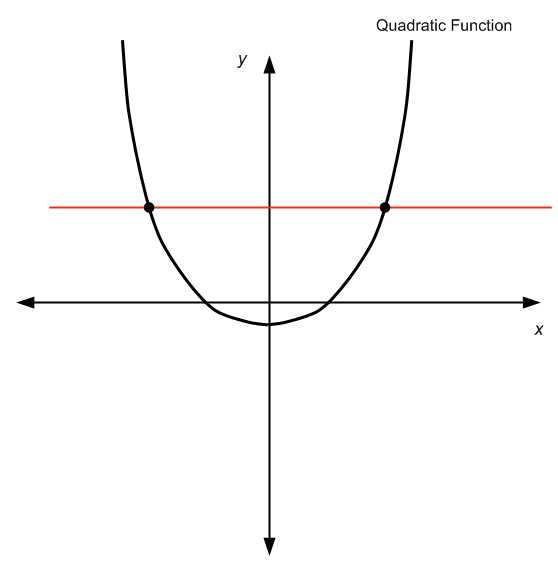
En ne passant pas le test de la ligne horizontale, nous pouvons voir que pour un \(y\) donné il y a plus d'une valeur \(x\) de sorte que \(f(x) = y\), donc nous ne pouvons pas "résoudre" pour \(x\), car il y en a plus d'un \(x\).
MAIS, si vous limitez le domaine et que vous ne considérez que les nombres positifs, nous obtiendrons ce qui suit:
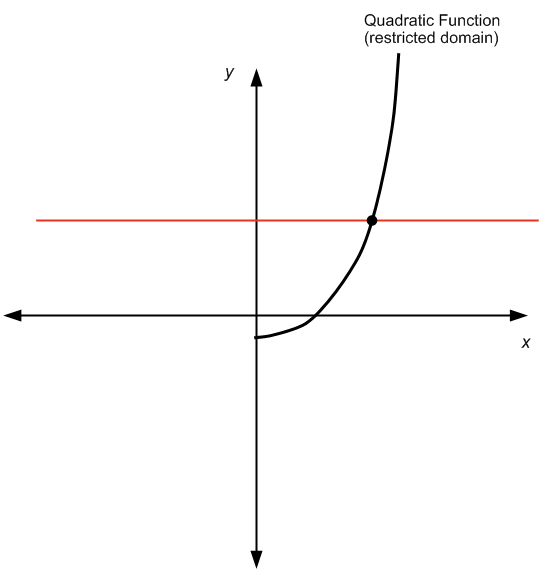
qui passe le test de la ligne horizontale, et par conséquent, la fonction quadratique est inversible.
MORALE DE L'HISTOIRE: Afin de vérifier si quelque chose est inversible, il ne s'agit PAS seulement de la fonction. Il s'agit de la fonction ET de sa domaine et plage .
Comment déterminer rapidement le graphique des fonctions inverses
Il est toujours nécessaire d'évaluer si la fonction \(f(x)\) est inversible ou non (en vérifiant si elle est ou non un-à-un). Mais en supposant que vous savez qu'il est inversible, il existe un moyen facile de trouver le graphique de l'inverse.
Tout d'abord, tracez le graphique de la fonction donnée \(f(x)\).
Ensuite, tracez le graphique de la ligne à 45 degrés \(y = x\).
Pour représenter graphiquement \(f^{-1}(x)\), tout ce que vous avez à faire est de refléter le graphique de \(f(x)\) à travers la ligne à 45 degrés \(y = x\), comme un miroir.
Voir l'exemple ci-dessous avec les fonctions \(f(x) = \sin x\) et \(f^{-1}(x) = \arcsin x\)
Une autre façon de voir cela est d'utiliser l'original graphique et modifiez la valeur de \(x\) par la valeur de \(y\).
Existe-t-il un moyen pour une fonction d'être son propre inverse?
Oui, c'est effectivement possible, mais cela n'arrive que pour la fonction d'identité, c'est-à-dire avec \(f(x) = x\).