Um Sistema de Equações é simplesmente um conjunto de duas ou mais equações simultâneas que precisam ser resolvidas. Normalmente, você terá o mesmo número de equações e incógnitas (variáveis), mas não precisa ser o caso.

A única coisa que está clara é que, para ter um sistema de equações, você precisa ter DUAS ou MAIS equações simultâneas. Por exemplo, o sistema abaixo

é um sistema de equações, com duas equações e duas incógnitas (\(x\) e \(y\)). Ou, por exemplo, o sistema abaixo:

é um sistema de equações, com duas equações e três incógnitas (\(x\), \(y\) e \(z\)).

O primeiro exemplo é um exemplo de um sistema de equações lineares.

O segundo exemplo é um exemplo de um sistema de equações não lineares. Por quê? Você adivinhou: o termo \(z^2\) na primeira equação o torna não linear.

Em termos gerais, a estratégia usada para resolver um sistema de equações depende se ele é linear ou não. Para sistemas lineares de equações, existem métodos sistemáticos para resolvê-los, como Regra de Cramer . Para sistemas não lineares de equações, não existe uma estratégia fixa e precisamos ir caso a caso.

Número de soluções de um sistema de equações

Quantas soluções um sistema de equações tem, se houver? Uma resposta geral a essa pergunta só pode ser dada no caso de sistemas de equações lineares, com base na relação entre o número de equações e o número de incógnitas.

Normalmente, em um sistema de equações lineares onde o número de equações é igual ou maior que o número de incógnitas, pode haver uma solução única, nenhuma solução ou soluções infinitas.

Quando o número de equações é menor que o número de incógnitas, pode haver um número infinito de soluções, ou nenhuma solução, mas não pode haver uma solução única.

Como você encontra um sistema de equações?

Esta questão está relacionada a como chegar a um sistema de equações. Existem vários contextos. Por exemplo, você pode estar lidando com um problema de palavras, no qual está produzindo três tipos diferentes de alimentos e tem vários tipos de restrições sobre esses alimentos em termos de custo, calorias, etc. Cada uma dessas restrições provavelmente pode ser representado como uma equação.

São inúmeras as aplicações em que diferentes restrições levam a equações lineares que precisam ser resolvidas simultaneamente, convertendo o problema em um sistema de equações.

EXEMPLO 1

Exemplo de sistema de equações: É o seguinte sistema de equações linear ou não linear?

RESPONDA:

Em primeiro lugar, o acima é um sistema de equações, com três equações e três incógnitas (\(x\), \(y\) e \(z\)). As duas primeiras equações são lineares se a última equação é não linear, por causa do termo \(\sin(z)\). Para ter uma equação linear, precisamos que as incógnitas sejam multiplicadas apenas por uma constante.

Portanto, o sistema de equações acima não é linear, mesmo que as duas primeiras equações sejam lineares, a terceira não é. Para um sistema, basta ter uma equação para não ser linear para que todo o sistema seja não linear.

EXEMPLO 2

Suponha que você produza três tipos de camisa nas seguintes quantidades: \(x\), \(y\) e \(z\). O tipo 1 tem um custo de $ 1, o tipo 2 tem um custo de $ 1,2 e o tipo 3 tem um custo de $ 1,5. Além disso, leva 1 hora para produzir o tipo 1, 0,5 horas para produzir o tipo 2 e 0,8 horas para o tipo de produto 3.

Eu sei que tenho $ 800 para gastar e 500 horas disponíveis. Além disso, com base em minhas estimativas de demanda, desejo produzir um total de camisetas do tipo 1 que seja a equação do total combinado do tipo 2 e tipo 3.

Escreva um sistema de equações com base nessas restrições. Este sistema é linear?

RESPONDA:

Observe que existem três incógnitas (\(x\), \(y\) e \(z\)), que corresponde ao número de camisas de cada tipo que precisam ser produzidas. Além disso, temos três equações: uma para o custo, uma para o número de horas disponíveis e uma para a restrição do número de camisas tipo 1 e os outros tipos.

As seguintes equações representam a situação:

Usando a convenção de deixar todos os termos que dependem das incógnitas no lado esquerdo, reescrevemos a última equação para obter:

Observe que cada equação é linear, então o sistema é um sistema de equações lineares.

Como você resolve sistemas de igualdades em geral?

Como foi mencionado acima, não existe uma estratégia única que se enquadrasse em todos os casos. Somente no caso de sistemas lineares de equação, haverá uma estratégia clara e bem definida.

Ainda assim, existem algumas boas práticas ou etapas que você deve seguir que podem ajudá-lo a resolver todos os tipos de sistemas de equações:

Passo 1: Identifique cada equação no sistema

Passo 2: Mova para um lado da equação todos os termos que dependem das incógnitas (normalmente para o lado esquerdo) e as constantes do outro lado

Etapa 3: Simplifique o lado esquerdo (com as incógnitas) e o lado direito (com as constantes)

Passo 4: Identifique a estrutura das equações. As equações são lineares ou não lineares?

Etapa 5: Se todas as equações são lineares, use uma das formas sistemáticas de resolver sistemas lineares (regra de Cramer, substituição, eliminação, redução de Gauss, etc)

Etapa 6: Se pelo menos uma equação for não linear, você pode tentar usar a abordagem de substituição, começando pela equação mais simples.

Mais sobre sistemas de equações

O sistema de equações aparece em toda parte em matemática, em todas as disciplinas. Ser capaz de resolver sistematicamente sistemas de equações provará ser uma habilidade crucial a dominar.

O sistema mais típico que você encontrará é um sistema de equações lineares. E freqüentemente, você encontrará sistemas de equações que são lineares, com duas equações e duas incógnitas. Esses sistemas são geralmente chamados de sistema 2x2 de equações lineares.

Sistema de representação gráfica de equações

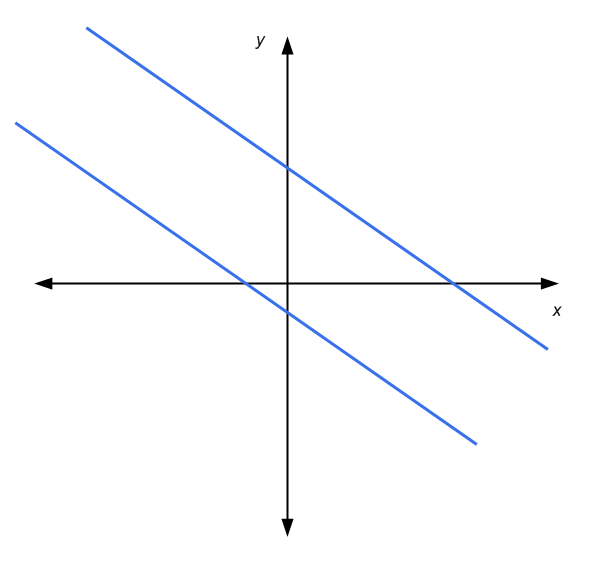
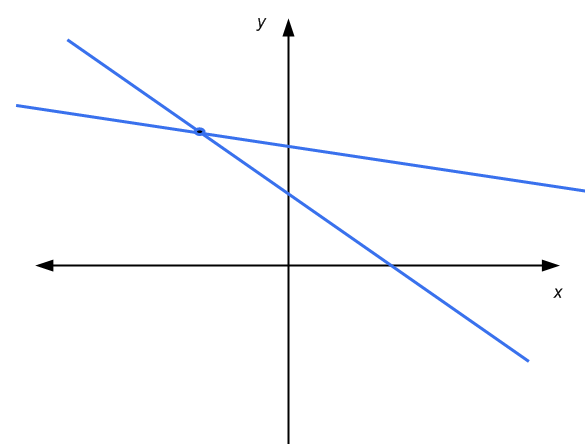
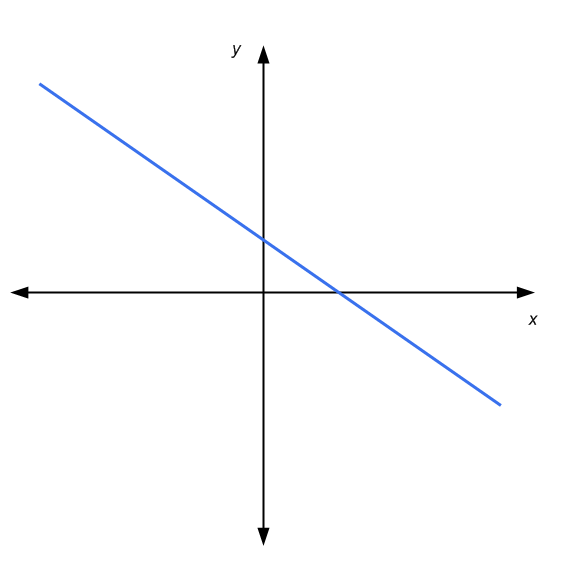
Para o sistema 2x2 de equações lineares, temos a vantagem de poder usar uma representação gráfica nos eixos coordenados. Uma equação linear é representada por uma linha no plano x-y. Graficamente, a solução de um sistema 2x2 é o ponto onde as duas linhas se cruzam, se houver.

Então, neste caso, temos que: as linhas são paralelas e não se tocam (nenhuma solução), as linhas se cruzam em um ponto (solução única), ou as linhas são paralelas e se tocam (infinitas soluções )

Calculadora de sistema de equações

Use este solucionador se quiser resolver um sistema 2x2 de equações lineares . Esta calculadora usa a regra de Cramer para resolver sistemas 2x2. Para sistemas maiores de equações, a melhor alternativa é usar o Método de eliminação gaussiana , que lida sistematicamente com sistemas lineares de qualquer tamanho.