Regra de Cramer
A regra de Cramer é uma técnica usada para resolver sistematicamente sistemas de equações lineares, com base nos cálculos de determinantes.
Normalmente, resolvendo sistemas de equações lineares pode ser confuso para sistemas maiores do que 2x2, porque existem muitas maneiras de contornar a redução quando há três ou mais variáveis.
A Regra de Cramer fornece uma maneira inequívoca e sistemática de encontrar soluções para sistemas de equações lineares, não importa o tamanho do sistema.
O número de cálculos necessários aumenta para sistemas grandes, mas o procedimento é exatamente o mesmo, independentemente do tamanho do sistema.
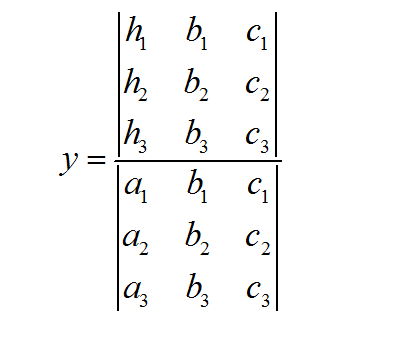
Como usar a regra de Cramer
Para tornar as coisas mais fáceis, resolveremos o caso de \(n = 2\) e então estabeleceremos uma versão mais geral que, esperançosamente, fará mais sentido depois de abordar o caso \(n=2\).
Passo 1
: Todos os sistemas lineares 2x2 podem ser escritos da seguinte forma:
Então, sua primeira etapa é encontrar esses valores \(a_1, b_1, c_1\) e \(a_2, b_2, c_2\) para o sistema que você deseja resolver.
Passo 2
: Depois de obter os coeficientes \(a_1, b_1, c_1\) e \(a_2, b_2, c_2\), você usa as seguintes fórmulas para resolver para \(x\) e \(y\):
Na fórmula acima, onde diz "det", significa o determinante da matriz correspondente. Às vezes, uma notação mais compacta é usada para determinantes, como mostrado abaixo:
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]Portanto, usando a notação acima, obteríamos essas fórmulas mais compactas para a regra de Cramer:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]Vamos ter uma maneira visual de entender o que está acontecendo. Observe que \(x\) e \(y\) têm o mesmo determinante no denominador.
Os coeficientes dessa matriz comum usada no denominador são derivados diretamente dos coeficientes que multiplicam \(x\) e \(y\) no sistema. Veja a imagem abaixo:
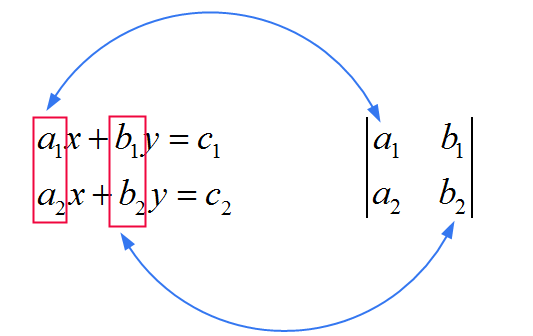
Agora vemos que \(x\) e \(y\) diferem no que têm no numerador. Como forma de lembrar a regra, pense no seguinte:
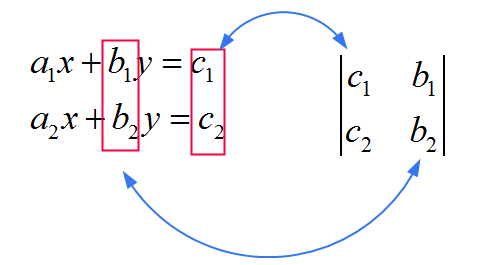
Para \(x\), você usa a MESMA matriz como a do denominador, apenas substituindo a coluna PRIMEIRA pelos coeficientes \(c_1\) e \(c_2\). Veja a imagem abaixo
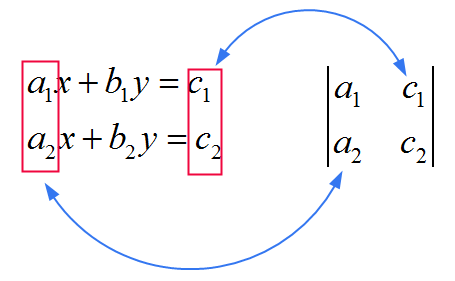
Para \(y\), você usa a MESMA matriz como a do denominador, apenas substituindo a SEGUNDA coluna pelos coeficientes \(c_1\) e \(c_2\). Veja a imagem abaixo
EXEMPLO 1
Resolva o seguinte sistema linear 2x2:
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]RESPONDA:
Vamos seguir as duas etapas que delineamos acima para usar a regra de Cramer para resolver o sistema acima:
Passo 1
: Precisamos identificar os coeficientes para os determinantes correspondentes.
Para a matriz que vai no denominador, usamos
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]Agora, neste caso \(c_1 = 10, c_2 = 4\), para o determinante usado para calcular \(x\), substituímos a matriz anterior alterando a coluna PRIMEIRA:
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]Para o determinante usado para calcular \(y\), substituímos a matriz anterior mudando a SEGUNDA coluna:
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]Portanto, agora temos a solução:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]e para \(y\):
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]Portanto, a solução é \(x = 3\), \(y = 1/2\).
Regra de Cramer para o caso geral
A beleza da regra de Cramer é que ela aplica exatamente o mesmo procedimento, seja um sistema 2x2 ou um sistema 10x10. O conceito é o mesmo.
Então, suponha que \(x_1, x_2, ..., x_n\) são as variáveis (as incógnitas), e queremos resolver o seguinte sistema n x n de equações lineares:
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]Para resolver \(x_1, x_2, ..., x_n\), usaremos o seguinte determinante no denominador:
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• A solução para \(x_1\) é
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• A solução para \(x_2\) é
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]E assim por diante. Como você pode ver, o determinante no denominador é o mesmo, e o determinante no numerador é obtido alterando a primeira coluna com \((c_1, ..., c_n)\) por \(x_1\). Para \(x_2\), alteramos a segunda coluna por \((c_1, ..., c_n)\), para \(x_3\) alteramos a terceira coluna e assim por diante. Você entendeu a ideia.
EXEMPLO 2
Resolva o seguinte sistema de equações lineares 3x3 usando a regra de Cramer.
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]RESPONDA:
Em primeiro lugar, identificamos o determinante que entra no denominador:
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]Além disso, precisamos identificar o vetor dos coeficientes \(c_i\):
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]Este vetor será o que estará substituindo as colunas correspondentes do determinante comum do denominador. Nós temos:
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]Mais sobre a regra de Cramer
A regra de Cramer tem um papel específico na solução eficiente de sistemas de equações lineares. Envolve o uso de determinantes para tornar muito simples uma tarefa que, de outra forma, seria realmente complicada, especialmente para sistemas maiores.
Em última análise, para resolver sistemas lineares , tudo o que você precisa fazer é identificar os determinantes de uma matriz numérica com base no sistema que precisa ser resolvido e realizar uma operação algébrica simples para resolver o sistema.
Formulários
A regra de Cramer tem muitas aplicações em Álgebra Linear e Equações Diferenciais.