Fórmula de arco-elasticidade para uma tabela

A fórmula da elasticidade do arco da demanda permite estimar a elasticidade nos pontos fornecidos em uma tabela de demanda, sem ter uma fórmula explícita para a função de demanda.

O que você precisa fornecer é uma tabela com uma coluna para preço e uma coluna para quantidade demandada. Uma vez que isso for digitado ou colado na planilha fornecida, você clicará em "Calcular" para obter as elasticidades de arco correspondentes computadas para você.

Observe que esta é apenas uma aproximação: a situação ideal é calcular elasticidades usando a função de demanda , usando derivadas.

Etapas para usar arc-elasticity para uma tabela

O fórmula de elasticidade do arco é:

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

e isso pode ser aplicado a pontos consecutivos em uma tabela de programação de demanda. Você seguirá estes passos:

• Passo 1: Tabule corretamente seus valores para preço (P) e quantidade demandada (Q)
• Passo 2: Você pode criar colunas para Q2 - Q1, P2 - P1, Q1 + Q2 e P1 + P2 se quiser tornar os cálculos mais claros, ou pode calcular a fórmula diretamente
• Etapa 3: Haverá um ponto ignorado na tabela, pois a elasticidade do arco pega um ponto na tabela e o ponto que imediatamente segue na tabela

Usar essa aproximação de arco-elasticidade fornecerá uma excelente imagem da sensibilidade às mudanças de preço do bem específico que está sendo analisado, mesmo que seja apenas uma aproximação.

Quanto mais pontos de demanda tivermos, melhor será a aproximação, especialmente se esses pontos de preço estiverem próximos.

O que a elasticidade do arco mede?

A elasticidade do arco visa fornecer uma aproximação da elasticidade real em um dado ponto. A elasticidade real da curva de demanda é calculada por:

\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]

Alguém poderia argumentar que a elasticidade do arco é apenas uma aproximação, então como ela tem algum valor? A resposta para isso é que para análise de elasticidade, e para análise de sensibilidade em Economia em geral, estamos mais interessados em intervalos do que em pontos muito específicos.

Na verdade, para fins de microeconomia, é útil saber se estamos ou não numa faixa inelástica, em vez do valor muito específico da elasticidade

Não é que o valor específico não seja importante, pois é realmente bom tê-lo, mas as elasticidades de arco geralmente são uma boa aproximação e nos darão representações muito precisas do tipo de intervalo de elasticidade que estamos enfrentando.

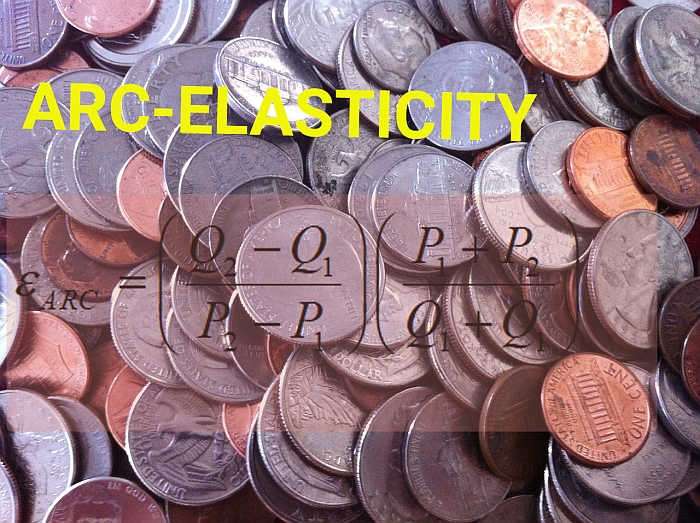
Exemplo

Considere a seguinte tabela de demanda com informações sobre preço e quantidade demandada

Forneça a aproximação da elasticidade do arco para os pontos de dados nesta tabela.

P	Pq
1	200
1.5	190
2	170
2.5	155
3	130
3.5	110
4	90
4.5	60

Solução: Para aproximar a elasticidade-preço da demanda a partir desses dados, precisamos usar a seguinte fórmula de arco-elasticidade

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

Ao aplicar a fórmula acima a todos os pares de pontos de dados consecutivos, encontramos as seguintes elasticidades de arco:

P	Pq	Elasticidade Do Arco
1	200	-
1.5	190	\(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\)
2	170	\(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\)
2.5	155	\(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\)
3	130	\(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\)
3.5	110	\(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\)
4	90	\(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\)
4.5	60	\(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\)

Interpretação

A tabela encontrada mostra a elasticidade-preço aproximada da demanda para cada um dos pontos de preço fornecidos. Esses valores podem ser usados aproximadamente para determinar faixas elásticas e inelásticas para o cronograma de demanda fornecido.

Outras calculadoras econômicas

Se você trabalha com Econometria, isso Calculadora de regressão provavelmente será útil, principalmente porque mostra todas as etapas do processo de cálculo de coeficientes de regressão .

Você também pode usar um equação log-log para estimar um curva de demanda com elasticidade constante .