Às vezes, uma pergunta simples como qual é a raiz quadrada de 64 tem uma resposta que pode confundir alguns.Neste caso, vamos dissipar um par de mitos.

O objetivo principal deste tutorial é aprender algumas coisas sobre raízes quadradas e radicais, para que você seja capaz de responder a perguntas sobre isso sem hesitação.

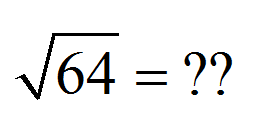
A primeira coisa é a primeira.Deixe-nos soletrar a definição da raiz quadrada:

A raiz quadrada de um determinado número é o positive número (ou zero) para que, quando o quadrado resultar nesse número dado .

É isso.Então, dado um número $x$, sua raiz quadrada é um número $b$ para que $b \ge 0$ e

Ao olhar para a expressão acima, podemos ver que, se $b$ for a raiz quadrada de $x$, então $x = b^2$, e como um número quadrado não pode ser negativo, $x$ só pode ser negativo (se quisermos ser capazes deEncontre sua raiz quadrada).

Conclusão : Só podemos calcular raízes quadradas de valores não negativos $x$.Ou disse diferentemente, o Domínio da Função. $\sqrt x$ é $[0,+\infty)$.

Então, respondendo a nossa pergunta inicial: Qual é a raiz quadrada de 64?

Com base no que definimos, precisamos encontrar um valor não negativo $b$ para que $b^2 = 64$.Qualquer número que atenda essas propriedades vêm à mente?

Bem, sim, e se tentássemos com $b = 8$?Ok, então $b = 8$ não é negativo e $b^2 = 8^2 = 64$.

Então, encontramos a raiz quadrada de 64, que é 8, porque 8 não é negativa, e $8^2 = 64$.Nós escrevemos isso como:

O mito sobre a função de raiz quadrada

Agora vamos ao tópico que motivou este tutorial ... a definição acima dada da raiz quadrada nos permite descartar a declaração comum de que "a raiz quadrada de 64 é mais ou menos 8", o que é errado.De fato

Agora, podemos entender por que esse mito carrega.De fato, ambos 8 e -8 têm a propriedade que $8^2 = 64$ e $(-8)^2 = 64$.Então, por que é -8 não a raiz quadrada de 64?

Porque por definição, dissemos que a raiz quadrada precisa ser aquele número não negativo que tenha a propriedade que quando se igualaram ao número dado.E -8 falha a condição de não ser negativo.

O gráfico da função de raiz quadrada

Olhe para o gráfico da função de raiz quadrada abaixo:

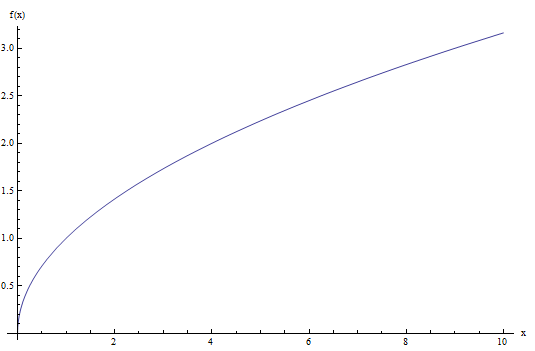
Como você pode ver, essa função só toma valores não negativos, e realmente passa o teste de linha vertical, por isso é uma função.

Então, no final, a definição da raiz quadrada como não negativa $b$ para que $b^2 = x$ torne a raiz quadrada uma função.

Se de fato tivéssemos que $\sqrt{64} = \pm 8$, então $\sqrt x$ não seria uma função, seria uma relação, porque a linha vertical em $x = 64$ cruzaria o gráfico duas vezes (a 8 e -8).

E quanto a outras funções radicais?

Existem outros tipos de funções radicais.Por exemplo, a raiz cúbica $\sqrt[3] x$.Nesse caso, não há necessidade de fazer uma regra para o que o radical escolher, porque a raiz cúbica de um determinado número $x$ é o número $b$ para que $b^3 = x$.

Raiz cúbica

Para o caso da raiz cúbica, não há necessidade de fazer distinções porque para um dado $x$ haverá apenas um número $b$ tal que $b^3 = x$.

Por exemplo

simplesmente porque $4^3 = 64$.Ou

simplesmente porque $(-4)^3 = -64$.Isto é, não há ambigüidade como no caso da raiz quadrada.

Raiz Quartic.

Para o caso de raiz de Quartic, é semelhante à raiz quadrada.Nós teremos isso $\sqrt[4] x = b$ se $b \ge 0$ e $b^4 = x$.

Por exemplo

Porque $2^4 = 16$ e $2 \ge 0$.Mas

Porque embora $(-2)^4 = -16$, temos isso $-2 < 0$ então a condição de não negatividade não é atingida.

Que tal para a raiz n-th $\sqrt[n] x$ em geral ???.

Tenho certeza que você adivinhou.

Para $n$ Mesmo, a situação é como a raiz quadrada: $\sqrt[n] x = b$ se $b \ge 0$ e $b^n = x$.

Para $n$ ímpar, a situação é como a raiz quadrada: $\sqrt[n] x = b$ se $b^n = x$.