Saiba mais sobre este criador de r-chart, a fim de compreender os resultados fornecidos por este gráfico.

Este criador do gráfico R fornecer-lhe-á todos os passos necessários para construir um gráfico R, que é normalmente utilizado para determinar se um processo está ou não em controlo estatístico.

Uma vantagem de utilizar este tipo de gráfico é que se pode indicar directamente se o processo não está sob controlo, dando uma vista de olhos e o gráfico, e identificando graficamente pontos que exibem um nível de variação que parece exceder o que é considerado como uma "causa comum" de variação.

Como posso calcular um gráfico r? que fórmulas devo usar

Você precisará fornecer um certo número de amostras, digamos que você forneça amostras \(N\), e cada uma das amostras tenha o mesmo tamanho de amostra, digamos que elas tenham um tamanho de amostra igual a \(k\).

Portanto, para as amostras, precisamos calcular a média amostral \(\bar X_i\) e o intervalo amostral correspondente \(R_i\). Portanto, no geral, temos médias de amostra \(N\) e intervalos de amostra \(N\). Finalmente, você encontra a média das médias amostrais, que você chama de \(\bar{\bar X}\) e a média dos intervalos amostrais, que você chama de \(\bar R\).

Depois de ter feito esses cálculos, pode utilizar as seguintes fórmulas para obter os limites de controlo (inferior e superior) para o gráfico R

\[ LCL_{R} = D_3 \bar R \] \[ UCL_{R} = D_4 \bar R \]

onde \(D_3\) e \(D_4\) são constantes que dependem do tamanho da amostra de cada amostra. Essas constantes precisam ser encontradas em tabelas de controle estatístico.

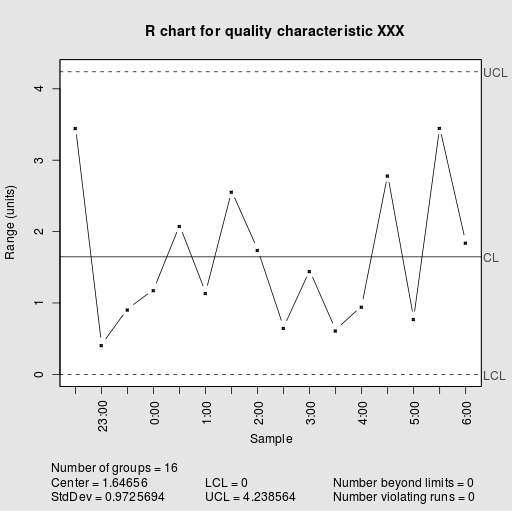
Em resumo: como se faz um gráfico r?

Passo 1. Primeiro recolhe-se os dados do que se está interessado em medir, e recolhe-se um certo número de amostras. Aqui assumimos que cada amostra tem o mesmo tamanho de amostra.

Passo 2. Depois de recolher os dados, é necessário calcular a média e o intervalo de amostragem, para cada uma das amostras que se tem.

Passo 3. Calcula-se a grande média para os meios e alcance da amostra.

Etapa 4. Em seguida, você usa as fórmulas fornecidas acima para calcular os limites de controle \(LCL_{R} = D_3 \bar R \) e \(UCL_{R} = D_4 \bar R \).

Passo 5. Num gráfico, é necessário traçar cada uma das gamas de amostras numa parcela de linha, e traçar também os limites inferior e superior.

Passo 6. Finalmente, a fim de determinar se alguma das gamas de amostras vai ou não além dos limites de controlo inferior e superior.

Os pontos que ultrapassam os limites de controlo inferior e superior estão fora de controlo estatístico. Quando não há nenhum ponto que esteja fora de controlo estatístico, então diz-se que o processo está sob controlo.

Outro gráfico de controlo

O gráfico R é utilizado para avaliar se a variabilidade do processo está ou não sob controlo. Se precisar de avaliar se o centro do processo se encontra em controlo estatístico, pode utilizar este Criador de gráficos de barras X .