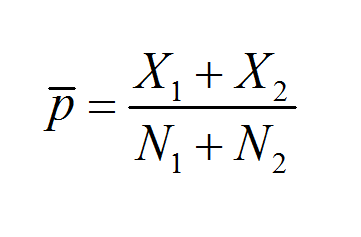Calculadora de proporções

Esta calculadora ajudará você com o cálculo de uma relação de proporcionalidade A / B = C / D, para a qual você precisa fornecer três das quatro expressões numéricas para encontrar a que falta. Além disso, você pode fornecer todas as quatro e a calculadora, nesse caso, avaliará se a proporcionalidade se mantém ou não para os números fornecidos.

Depois de fornecer as expressões numéricas solicitadas (que podem ser números ou qualquer expressão numérica válida), você pode clicar no botão "Calcular" para ver o resultado dos cálculos.

Como usar esta calculadora de proporções?

Usar esta calculadora de proporções simplificará a resolução de proporções matemáticas para você. Aqui estão os passos que você deve seguir:

• Identifique a proporcionalidade: Estabeleça a proporção que você precisa calcular
• Insira os valores conhecidos: Insira os valores conhecidos nas caixas fornecidas. Você precisa de três números dos quatro envolvidos na proporção.
• Calcular: Clique no botão calcular para obter o resultado. A calculadora mostrará o valor faltante.

Passos para resolver proporções

Veja como você pode resolver proporções manualmente:

• Configure a proporção: Escreva as proporções em forma de fração, como \(\frac{A}{B} = \frac{C}{D}\).
• Multiplicação Cruzada: Multiplique o numerador da primeira fração pelo denominador da segunda, e vice-versa: \(A \times D = B \times C\).
• Resolva o desconhecido: Se você estiver resolvendo para \(x\), reorganize a equação para isolar \(x\).
• Verifique Seu Trabalho: Certifique-se de que as proporções sejam iguais substituindo o valor encontrado de volta na proporção original.

Fórmula de proporção explicada

A fórmula básica para uma proporção é:

\[ \frac{A}{B} = \frac{C}{D} \]

Onde \(A\) e \(B\) são a primeira razão, e \(C\) e \(D\) são a segunda razão. Esta fórmula também pode ser expressa como tendo o produto \(B \times C\)) igual ao produto de \(A \times D\)). Esta relação desempenha um papel fundamental na compreensão de como as proporções funcionam.

Tipos de proporções

Existem vários tipos de proporções:

• Proporção Direta: Quando uma quantidade aumenta, a outra aumenta na mesma taxa. Por exemplo, se você dobra o número de trabalhadores, o trabalho feito também dobra.
• Proporção Inversa: À medida que uma quantidade aumenta, a outra diminui. Por exemplo, se você aumenta a velocidade da viagem, o tempo para chegar a um destino diminui, por causa da fórmula física tempo = distância / velocidade.
• Proporção Partitiva: Usado ao dividir um todo em partes de acordo com proporções fornecidas.

Proporção direta vs. proporção inversa

Um tópico muito importante de entender é a diferença quantitativa entre proporções diretas e inversas:

• Proporção Direta: Quando \(x\) é diretamente proporcional a \(y\), temos \(x = ky\) onde \(k\) é uma constante.
• Proporção Inversa: Quando \(x\) é inversamente proporcional a \(y\), temos \(xy = k\), onde \(k\) é uma constante.

Aplicações de proporções na vida real

Proporções não são apenas uma construção teórica e podem ter inúmeras aplicações práticas, incluindo:

• Culinária: Aumentar ou diminuir receitas com base no número de porções.
• Financiar: Calcular taxas de juros ou retornos de investimentos.
• Construção: Determinar a quantidade de materiais necessários para um projeto.
• Medicamento: Cálculos de dosagem com base no peso ou idade do paciente.

Como calculo uma proporção?

Para calcular uma proporção:

• Identifique os valores conhecidos na proporção.
• Configure a equação de proporção.
• Use a multiplicação cruzada para resolver a incógnita.
• Verifique sua solução substituindo-a novamente na equação original.

As proporções 14:7 e 8:4 formam uma proporção?

Precisamos verificar isso:

\[ \frac{14}{7} = \frac{8}{4} \]

Simplificando, obtemos simplesmente:

\[ 2 = 2 \]

o que implica que ambos os lados são iguais. Então, sim, as razões 14:7 e 8:4 formam uma proporção porque são iguais quando simplificadas.

15, 2 e 4/30 formam uma proporção?

Para verificar:

\[ \frac{15}{2} = \frac{4}{30} \]

Simplificando:

\[ \frac{15}{2} = 7.5 \] \[ \frac{4}{30} = \frac{2}{15} = 0.1333 \]

Portanto, a resposta é NÃO, elas não formam uma proporção, pois as razões não são iguais.

Calculadora de proporções com passos

Veja como funciona nossa calculadora de proporções com etapas:

• Insira os valores conhecidos, que geralmente são 3 dos 4 valores.
• A calculadora mostrará o processo passo a passo para resolver a proporção com base nas entradas fornecidas, o que inclui qualquer multiplicação cruzada necessária e a resolução da variável desconhecida.
• Ele fornecerá a resposta final para o valor desconhecido, juntamente com as etapas tomadas para chegar à resposta.

Calculadora de proporções com 2 variáveis

Ao lidar com duas variáveis em uma proporção, a situação é um pouco diferente porque você não pode resolver imediatamente uma variável, mas prefere expressar uma das incógnitas em termos da outra:

• Etapa 1: você precisa configurar a equação com os valores conhecidos e as variáveis.
• Etapa 2: Em seguida, você usará manipulação algébrica para resolver uma variável em termos da outra.
• Etapa 3: Por fim, você deve inserir o valor conhecido para encontrar a variável desconhecida.

Calculadora de proporção de fração

Muitas vezes você pode considerar proporções como frações . Uma calculadora de proporção de fração ajuda em:

• Converter frações em decimais ou porcentagens para facilitar a comparação.
• Verificar se frações são equivalentes simplificando-as.
• Resolvendo frações desconhecidas em uma proporção.

Proporções em matemática

Você descobrirá que as proporções desempenham um papel significativo em vários campos matemáticos, incluindo os seguintes:

• Geometria: Triângulos semelhantes e escala aplicarão diretamente proporções entre os lados
• Álgebra: Resolvendo equações envolvendo razões. Isso também pode ocorrer em Cálculo, ao lidar com taxas relacionadas
• Estatísticas: Usado para entender diferentes relações proporcionais em conjuntos de dados. Geralmente analisado na forma de proporções de amostra.

Ao entender e aplicar proporções, você pode resolver problemas complexos em matemática e cenários do mundo real com facilidade. Não importa se você está ajustando uma receita, calculando retornos financeiros ou dimensionando um projeto, as proporções são suas aliadas matemáticas.

Mais calculadoras de proporções

Se você estiver trabalhando com proporções, pode ser útil também tropeçar em áreas relacionadas, como proporções de amostra. Nosso Calculadora De Proporção De Amostra pode ajudar você a entender como as proporções funcionam e são calculadas dentro de uma amostra, o que é particularmente útil em análises estatísticas ou ao lidar com pesquisas e enquetes.

Além disso, se o seu trabalho envolve análise financeira, métricas de negócios ou se você simplesmente deseja começar com demonstrações financeiras e sua interpretação, nosso Calculadora De Razão Rápida pode ser de interesse. Ajuda a avaliar a capacidade de uma empresa de cumprir suas obrigações de curto prazo com seus ativos mais líquidos, o que indiretamente se relaciona com a compreensão de proporções em termos financeiros.

Por fim, para aqueles que costumam converter entre diferentes formas de números, nosso Calculadora de Fracção para Percentagem e Calculadora de Percentagem para Fracção pode simplificar essas conversões, garantindo que você tenha as ferramentas certas para trabalhar com proporções em vários formatos.